Radiométrie, photométrie

Une grandeur spectrale dépend de sa longueur d’onde, à savoir la distance en mètres nécessaire à la répétition d’un motif élémentaire. On donne $\mathrm{\lambda_0=\frac{c}{ν}=c \times T}$ avec :

• $\mathrm{\lambda_0}$ la longueur d’onde en mètres
• $\mathrm{c}$ la célérité de la lumière en $\mathrm{m.s^{-1}}$
• $\mathrm{v}$ la fréquence de l’onde en $\mathrm{Hz}$

Un objet peut être soit une source primaire, responsable de l’éclairement (étoile, lampe) ou une source secondaire, diffusant la lumière issue d’une autre source primaire (table, chaise, …)

La lumière blanche présente un spectre continu entre $400$ et $\mathrm{800~nm}$. Toutes les longueurs d’ondes sont émises. Cependant, il existe des dispositifs ne présentant qu’une ou plusieurs « raies » d’émission. Ce sont des spectres discontinus, caractéristiques des éléments utilisés.

• lampe à sodium (monochromatique) : $1$ raie à $\mathrm{590~nm}$
• lampe à mercure (polychromatique) : $7$ raies principales à $\mathrm{405~nm, 436~nm, 546~nm, 577~nm, 579~nm, 580~nm, 615~nm}$

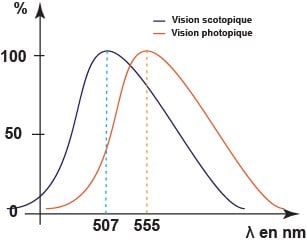
En termes de sensibilité spectrale, l’œil humain capte mieux les longueurs d’ondes de $\mathrm{555~nm}$ (vert) en vision diurne et $\mathrm{507~nm}$ (bleu) en vision nocturne.

Pour caractériser la lumière, on utilise les grandeurs suivantes :

• $\mathrm{\Delta \Phi}$, le flux (lm, W) : c’est le débit de lumière le long d’un rayon
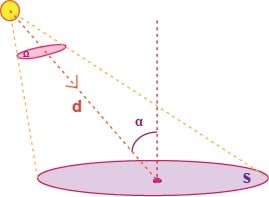
• $\mathrm{I}$, intensité $\mathrm{(cd, W.sr^{-1})}$  : c’est le flux de lumière émis par unité d’angle solide $\mathrm{\Omega}$

$\mathrm{\displaystyle I=\frac{\Phi_{émis}}{\Omega}}$ et $\mathrm{\Omega =\frac{S \times \cos \alpha}{d^2}}$

• $\mathrm{L}$, luminance $\mathrm{(cd.m^{-2}, W.sr^{-1}.m^{-2})}$ : c’est l’intensité lumineuse émise par unité de surface apparente de la source.
• $\mathrm{E}$, éclairement $\mathrm{(lux, W.m^{-2})}$ : c’est le flux reçu par unité de surface

$\mathrm{E=\frac{\Phi_{émis}}{S}}$ et $\mathrm{E=\frac{I \times \cos\alpha}{d^2}}$

Le collecteur de flux doit permettre de capter tout le flux issu de la source sans en reconstituer une géométrie parfaite. Un capteur d’image doit au contraire reconstituer la géométrie d’une image.