La diffraction est un phénomène inévitable qui produit des limites non nettes des images. Il a l’inconvénient de limiter la résolution des instruments optiques, mais l’avantage de décomposer les spectres lumineux.
Lorsqu’un faisceau lumineux rencontre un obstacle, il ne suit plus une propagation rectiligne, mais suit le principe d’Huygens – Fresnel, selon lequel la lumière se propage en formant une nouvelle onde sphérique au point suivant. L’onde suit alors les différentes interférences produites entre toutes ces ondes.
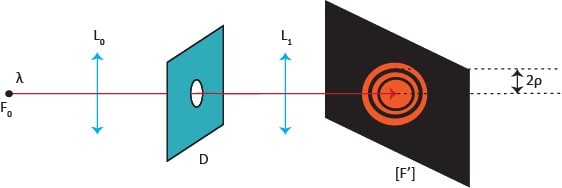
Diffraction par une ouverture circulaire
Quand un faisceau traverse un diaphragme de diamètre d, on obtient une figure de diffraction constituée d’une tache centrale très lumineuse, appelée tache d’Airy de rayon ρ, encerclée de différents cercles concentriques.
La tache d’Airy est d’autant plus grande que
- d est petit
- λ est grande
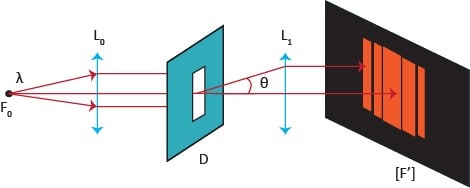
Diffraction par une fente fine
Lorsque l’obstacle est une fente fine, la tache centrale est beaucoup plus lumineuse. On remarque sur le graphique d’intensité que la frange centrale est deux fois plus large que les taches diffractées, et que les minima d’intensité se situent à sinθ=mλD avec m un entier relatif non nul.
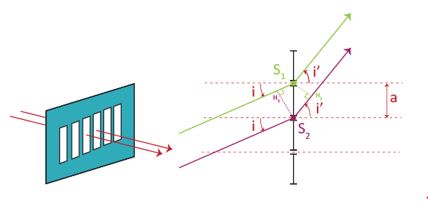
Diffraction par un réseau par transmission
La différence de marche est dans ce cas :
avec un entier relatif (on a choisi pour obtenir les maxima principaux grâce à des interférences constructives.
A , on obtient un rayon non dévié avec un maximum d’intensité lumineuse pour .
Pouvoir séparateur
Deux images sont séparées l’une de l’autre à condition qu’une tache d’Airy corresponde au premier minimum de l’autre. Dans ce cas, l’instrument possède un bon pouvoir séparateur. Le pouvoir séparateur est inversement proportionnel à la limite de résolution.
Le pouvoir de résolution détermine la distance à laquelle deux points sont distincts. Il dépend en partie du phénomène de diffraction, mais aussi de la taille des grains d’une émulsion pour un négatif photographique ou la définition du capteur pour un capteur photo numérique.
L’ouverture, la distance de mise au point et la longueur focale permettent de calculer la profondeur de champ et déterminer les zones floues et nettes.
La limite de résolution œil-instrument se résout à étudier le phénomène de diffraction de l’instrument d’une part, et la limite du capteur due à la taille des pixels ou des grains argentiques et à prendre la plus grande résolution des deux.