Polarisation

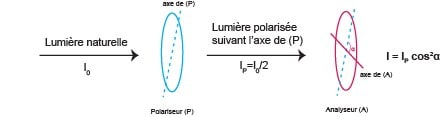
La lumière naturelle n’est pas polarisée : ses vibrations suivent toutes les directions possibles. Il est possible de la polariser linéairement dans une direction privilégiée grâce à un filtre polariseur.

Si on ajoute un 2ème polariseur après un premier $\mathrm{(P)}$, il se nommera « analyseur » $\mathrm{(A)}$ et permettra de contrôler l’intensité du faisceau émergent. La loi de Malus nous donne l’intensité finale :

$\mathrm{I_A=I_P \times \cos^2 \alpha, avec ~{I_P=\frac{I_0}{2}}}$

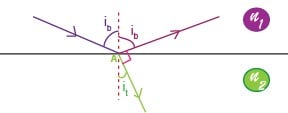
Quand la lumière est réfléchie face à un dioptre séparant 2 milieux d’indices respectifs $\mathrm{n_1}$ et $\mathrm{n_2}$ , elle est polarisée rectilignement, dans une direction perpendiculaire au plan d’incidence, à condition que le rayon transmis et le rayon réfléchis soient eux-mêmes perpendiculaires. On a donc :

$\mathrm{i_b + i_t = 90°}$. 

En injectant cette condition dans la 2ème loi de Descartes, on obtient la loi de Brewster :

$\mathrm{\tan⁡i_b=\frac{n_2}{n_1}}$

Il existe un cas de bi réfringence où un cristal est capable de dédoubler les faisceaux lumineux. Il se produit alors :

• un rayon ordinaire, issu de la réfraction normale, polarisée rectilignement $\mathrm{(R_0, n_0)}$
• un rayon extraordinaire, issu d’une réfraction anormale d’indice variable entre $\mathrm{n_0}$ et ne, polarisée rectilignement, de direction perpendiculaire à celle du rayon ordinaire.

Comme l’indice $\mathrm{n}$ dépend de la direction de polarisation, un tel cristal est anisotrope.