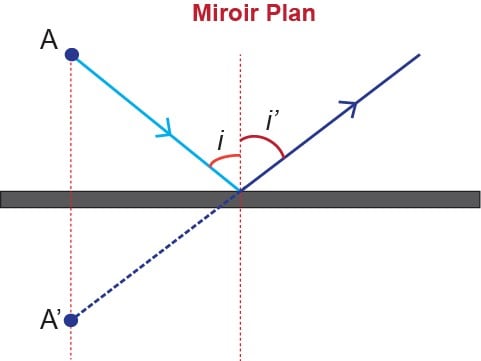
Miroir plan :
- L’angle incident $\mathrm{i}$ est égal à l’angle réfléchi $\mathrm{i'}$
- L’image d’un objet réel est virtuelle et l’image d’un objet virtuel est réelle (projetable sur un écran)
- Par extension, l’image de tout objet est son symétrique par rapport à la normale au miroir. L’image et l’objet sont non chiraux (non superposables)
- Quand le miroir est incliné d’un angle $\mathrm{\alpha}$, son image l’est d’un angle $\mathrm{2 \alpha}$
- Lorsqu’un miroir plan réalise une translation selon un vecteur $\mathrm{\vec V}$, l’image subit une translation selon le vecteur $\mathrm{2 \vec V}$
- C’est le seul dispositif optique à être rigoureusement stigmatique
Miroir sphérique :
- Le foyer objet (miroir concave) ou image (miroir convexe) est toujours situé au milieu du segment [CS]
- Les seuls points rigoureusement stigmatiques sont C et tous les points appartenant à la surface du miroir
- Les points cardinaux sont C (Centre optique), F (Foyer objet) et F’ (Foyer image)
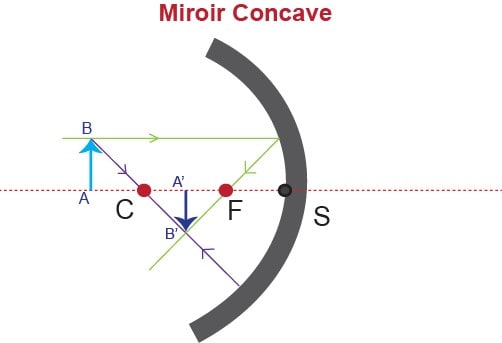
- Pour construire l’image d’un objet plan :
- Tracer le rayon issu de B passant par C (le rayon n’est pas dévié lors de la réflexion)
- Tracer le rayon issu de B parallèle à l’axe CS, passant par F en se réfléchissant
- L’image est parallèle à l’objet et l’image du point en dehors de l’axe CS (B) est à l’intersection des 2 rayons (B’)
- Formule de conjugaison de Descartes (origines au sommet, le sens positif est celui de la lumière)
- $\mathrm{\frac{1}{\overline {SA'}} + \frac{1}{\overline {SA}} =\frac{1}{\overline {SF}}}$
- $\mathrm{\gamma=-\frac{\overline{SA'}}{\overline{SA}}}$
- Formule de conjugaison de Newton (origines aux foyers)
- $\mathrm{\overline{FA} \times \overline {FA'}=\overline{SF}^2}$
- $\mathrm{\gamma =-\frac{\overline {FA'}}{\overline {SF}} =\frac{\overline{SF}}{\overline {FA}}}$
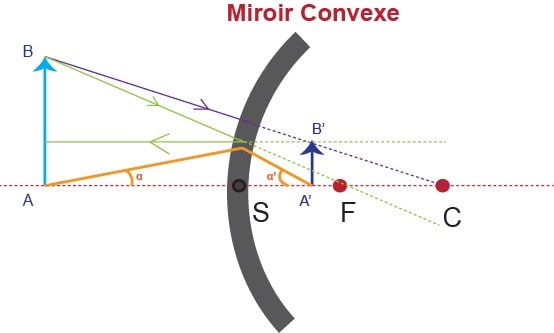
- Relation de Lagrange-Helmholtz (ex schéma du miroir convexe)
- $\mathrm{\alpha \overline {AB}=-\alpha'\overline{A'B'}}$
- Grossissement angulaire $\mathrm{G=\frac{α'}{α} =-\frac{1}{\gamma}}$
