Optique (S2)

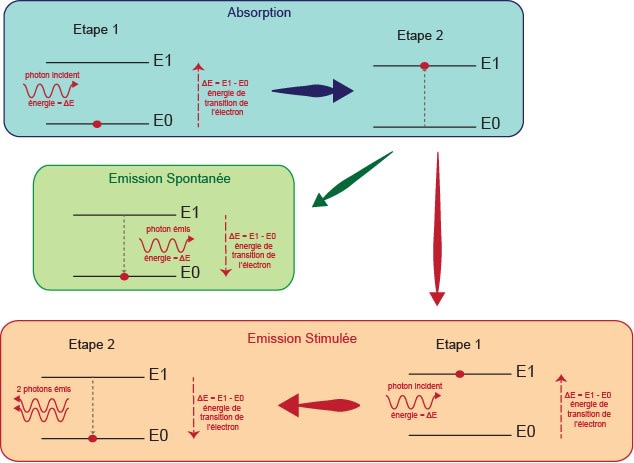
L’émission spontanée se fait de façon aléatoire en temps (on ne sait pas quand le photon sera émis) et en terme de direction (on ne sait pas dans quelle direction le photon sera émis). L’énergie du photon émis est égale à $\mathrm{\Delta E=\frac{h \times c}{\lambda}}$ avec :

$\mathrm{h}$ : la constante de Planck $\mathrm{h = 6,63.10^{-34}~ J.s}$ 
$\mathrm{c}$ : la célérité de la lumière dans le vide $\mathrm{c \approx 300~ 000~ km.s^{-1}}$
$\mathrm{\lambda}$ : la longueur d’onde du photon

L’émission stimulée se fait lorsqu’un électron déjà excité dans un état $\mathrm{E_2}$ va rencontrer un photon d’exacte énergie $\mathrm{\Delta E= E_2 – E_1}$, ce qui va permettre l’émission de $2$ photons identiques, de même énergie, fréquence et phase pour que l’électron revienne au niveau $\mathrm{E_1}$. C’est le principe de fonctionnement du Laser.

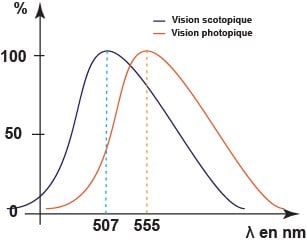
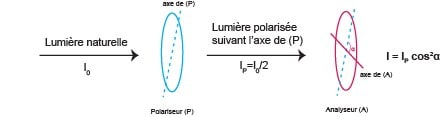
La lumière est de deux natures : 

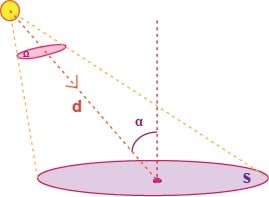
• Corpusculaire (elle véhicule des photons) : caractérisée par son flux, son intensité, sa luminance, et son éclairement
• Ondulatoire (c’est également une onde) : caractérisée par sa fréquence et sa période (périodicité temporelle) sa longueur d’onde et sa vitesse de propagation (périodicité spatiale)

$\mathrm{f= \frac{1}{T}}$

$\mathrm{\lambda_0= c \times T = \frac{c}{f}}$

Les deux principes fondamentaux de l’optique géométrique découlent du chemin optique $\mathrm{L_{AB}=c \times \tau = n\overline{AB}}$, avec : 

$\mathrm{c}$ la célérité de l’onde
$\mathrm{\tau}$ le temps de parcours de l’onde
$\overline{AB}$ la valeur algébrique de la distance AB
$\mathrm{n=\frac{c}{v}}$ l’indice de réfraction du milieu

Le principe de Fermat : le trajet de la lumière correspond à une valeur indépendante du temps du chemin optique $\mathrm{L_{A\rightarrow B}}$ 

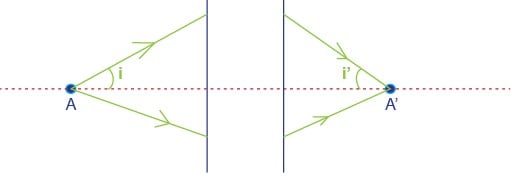
• Principe de retour inverse de la lumière : la direction est toujours la même quelque soit le sens de la lumière
• La trajectoire est rectiligne dans un milieu homogène et isotrope.

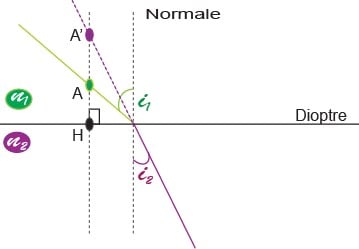
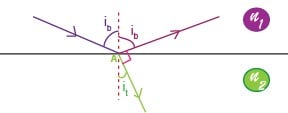
Les lois de Descartes :

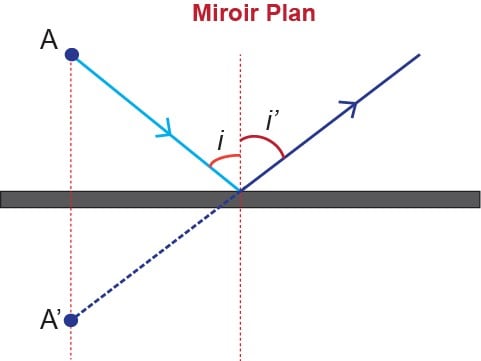
• Réflexion
• 1ère loi : Le rayon réfléchi est dans le plan d’incidence
• 2ème loi : L’angle d’incidence (entre le rayon incident et la normale à la surface) est égal à l’angle réfléchi (entre le rayon réfléchi et la normale à la surface)
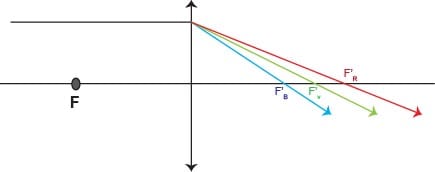
• Réfraction
• 1ère loi : Le rayon réfracté est dans le plan d’incidence
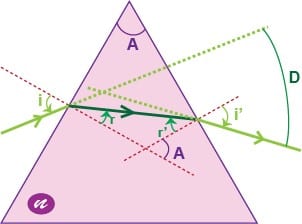
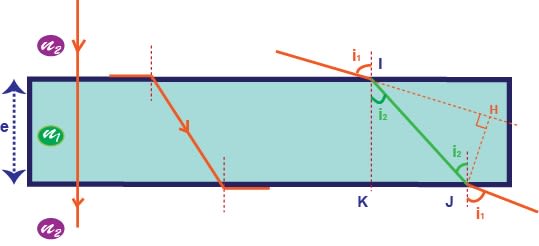
• 2ème loi : $\mathrm{n_1 \sin(i_1) = n_2 \sin (i_2)}$ avec $\mathrm{n_1}$ et $\mathrm{n_2}$ les indices de réfraction des $2$ milieux, $\mathrm{i_1}$ l’angle incident et $\mathrm{i_2}$ l’angle entre la normale et le rayon réfracté
• Dans le cas où $\mathrm{n_2 < n_1}$, il n’y a plus de réfraction au-delà de l’angle limite $\mathrm{i_L=\sin^{-1} \frac{n_2}{n_1}}$. C’est la réflexion totale (utilisée dans la fibre optique).

Cas d’un dioptre plan

Un dioptre sépare deux milieux transparents, homogènes et isotropes, d’indices de réfraction n différents. On rappelle $\mathrm{n=\frac{c}{v}}$ avec $\mathrm{c}$ la célérité de la lumière dans le vide et $\mathrm{v}$ la vitesse de la lumière dans le milieu considéré.

Dans un système optique utilisant un dioptre :

• Le principe de propagation rectiligne de la lumière n’est pas respecté : loi de Descartes $\mathrm{n_1 \sin⁡(i_1 )=n_2 \sin⁡(i_2)}$ ou encore loi de Kepler quand l’angle $\mathrm{i_1}$ est très proche de la normale $\mathrm{n_1 \times ⁡(i_1 )= n_2 \times ⁡(i_2)}$
• Dans le cas où $\mathrm{n_2 < n_1}$, il est possible d’obtenir une réflexion totale, pour les angles supérieurs à $\mathrm{i_L=\sin^{-1}⁡ \frac{n_2}{n_1}}$
• Le principe de retour inverse reste valable quelque soit le nombre de réfractions et de réflexions subies.
• Lorsqu’un objet est parallèle au dioptre, son image conserve la même dimension. Le grandissement est donc égal à $\mathrm{+1}$. Quand il lui est perpendiculaire, son grandissement $\mathrm{\gamma =\frac{n_2}{n_1}}$ 
• La relation de conjugaison devient $\mathrm{\frac{n_1}{\overline{HA}} = \frac{n_2}{\overline {HA'}}}$.

Cas du prisme

Le prisme est entièrement défini par son angle A et son milieu n. Les formules du prisme sont les suivantes :

$\mathrm{\sin⁡(i)=n\times \sin⁡(r)}$

$\mathrm{\sin⁡(i' )= n \times \sin⁡(r' )}$

$\mathrm{r+r'=A}$

$\mathrm{D=i+i'-A}$

Comme la sortie du rayon du prisme se fait d’un milieu plus réfringent vers un milieu moins réfringent, il existe un angle limite au-delà duquel il n’y aura plus d’émergence. Donc la condition d’émergence est la suivante : 

$\mathrm{-r_L' \leq r'\leq r_L'}$

Soit $\mathrm{-r_L' \leq A-r \leq r_L'}$

Concernant la déviation D :

• Elle est fonction croissante de A
• Elle décroît avec l’angle d’incidence jusqu’à un minimal $\mathrm{i_m=\frac{A+D_m}{2}}$ puis croît jusqu’à $\mathrm{i=90°}$.

• En réinjectant la loi de Descartes, nous pouvons déterminer n à partir de im et $\mathrm{A : n=\frac{\sin⁡(\frac{A+D_m)}{2}}{\sin⁡(\frac{A}{2})}}$.

Cas d’une lame à faces parallèles $\mathrm{(n_2 < n_1)}$

Dans le cas d’utilisation de lames parallèles, on considère chacune des faces comme un dioptre, d’indice $\mathrm{n_1}$ , étant environnées d’un même milieu d’indice $\mathrm{n_2}$.

Un rayon lumineux traversant une lame à faces parallèles n’est pas dévié. Il est simplement déplacé (sauf dans le cas où le rayon est normal à la surface). Le déplacement latéral est proportionnel à l’épaisseur $\mathrm{e}$ :

$\mathrm{HJ=e \frac{\sin⁡(i_1-i_2)}{\cos⁡(i_2)}}$

Le grandissement linéaire est égal à $\mathrm{+1}$.

Un système optique sépare l’espace entre un plan objet (en amont) et un plan image (en aval).
Quand un objet est vu :

• Dans le plan objet, il est réel 
• Dans le plan image, il est virtuel 

Quand une image est vue :

• Dans le plan image, elle est réelle (lampe face à un miroir, se reflétant sur un écran)
• Dans le plan objet, elle est virtuelle (objet face à un miroir)

Les images sont parfaitement formées quand :

• Le stigmatisme est rigoureux : l’image d’un point est un point et non une tâche
• Le système est aplanétique : l’image d’une droite perpendiculaire à l’axe optique est également perpendiculaire.

Pour pouvoir obtenir des résultats satisfaisants en optique géométrique, il faut respecter les conditions de Gauss :

• Les objets sont plans et perpendiculaires à l’axe optique (aplanétisme)
• Les rayons sont peu inclinés par rapport à l’axe optique (stigmatisme approché). Comme les angles incidents sont très faibles, ils sont assimilables à leurs sinus $\mathrm{(\sin i \approx i)}$. La loi de Descartes $\mathrm{n_1 \times \sin i_1 = n_2 \times  \sin i_2}$ peut alors s’écrire comme la loi de Kepler $\mathrm{n_1 \times i_1 = n_2 \times i_2}$.
  

Miroir plan :

• L’angle incident $\mathrm{i}$ est égal à l’angle réfléchi $\mathrm{i'}$
• L’image d’un objet réel est virtuelle et l’image d’un objet virtuel est réelle (projetable sur un écran)
• Par extension, l’image de tout objet est son symétrique par rapport à la normale au miroir. L’image et l’objet sont non chiraux (non superposables)
• Quand le miroir est incliné d’un angle $\mathrm{\alpha}$, son image l’est d’un angle $\mathrm{2 \alpha}$
• Lorsqu’un miroir plan réalise une translation selon un vecteur $\mathrm{\vec V}$, l’image subit une translation selon le vecteur $\mathrm{2 \vec V}$
• C’est le seul dispositif optique à être rigoureusement stigmatique

Miroir sphérique :

• Le foyer objet (miroir concave) ou image (miroir convexe) est toujours situé au milieu du segment [CS]
• Les seuls points rigoureusement stigmatiques sont C et tous les points appartenant à la surface du miroir
• Les points cardinaux sont C (Centre optique), F (Foyer objet) et F’ (Foyer image)
• Pour construire l’image d’un objet plan :
• Tracer le rayon issu de B passant par C (le rayon n’est pas dévié lors de la réflexion)
• Tracer le rayon issu de B parallèle à l’axe CS, passant par F en se réfléchissant
• L’image est parallèle à l’objet et l’image du point en dehors de l’axe CS (B) est à l’intersection des 2 rayons (B’)
• Formule de conjugaison de Descartes (origines au sommet, le sens positif est celui de la lumière)
• $\mathrm{\frac{1}{\overline {SA'}} + \frac{1}{\overline {SA}} =\frac{1}{\overline {SF}}}$ 
• $\mathrm{\gamma=-\frac{\overline{SA'}}{\overline{SA}}}$ 
• Formule de conjugaison de Newton (origines aux foyers)
• $\mathrm{\overline{FA} \times \overline {FA'}=\overline{SF}^2}$
• $\mathrm{\gamma =-\frac{\overline {FA'}}{\overline {SF}} =\frac{\overline{SF}}{\overline {FA}}}$ 
• Relation de Lagrange-Helmholtz (ex schéma du miroir convexe)
• $\mathrm{\alpha \overline {AB}=-\alpha'\overline{A'B'}}$
• Grossissement angulaire $\mathrm{G=\frac{α'}{α} =-\frac{1}{\gamma}}$
  

Un dioptre sphérique sépare un milieu transparent objet d’indice $\mathrm{n_1}$ d’un milieu transparent image d’indice $\mathrm{n_2}$. Il est caractérisé par son demi-angle d’ouverture $\mathrm{\alpha}$.

Pour construire une image, il faut respecter les caractéristiques suivantes :

• C est sa propre image
• Tout rayon issu de C n’est pas dévié
• Un rayon parallèle à l’axe optique est réfracté en passant par le foyer image F’
• Un rayon passant par le foyer objet F sera réfracté parallèle à l’axe optique

Un dioptre concave avec $\mathrm{n_1 > n_2}$ sera donc convergent (foyer image réel). Un dioptre concave avec $\mathrm{n_1 < n_2}$ sera divergent.

Un dioptre convexe avec $\mathrm{n_1 > n_2}$ sera donc divergent (foyer image virtuel). Un dioptre convexe avec $\mathrm{n_1 < n_2}$ sera convergent.

Les formules de conjugaison et de grandissement sont les suivantes (le sens positif est celui de la marche des rayons) :

• Origine aux centres :
  $\mathrm{\frac{n_1}{\overline {CA'}} -\frac{n_2}{\overline{CA}} = \frac{n_1-n_2}{\overline{CS}}, {\gamma =\frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline {CA'}}{\overline{CA}}}}$
• Origine aux sommets (Descartes) :
  $\mathrm{\frac{n_1}{\overline{SA}} -\frac{n_2}{\overline{SA'}} = \frac{n_1-n_2}{\overline{SC}}, \gamma = \frac{\overline{A'B'}}{\overline{AB}} = \frac{\overline {SA'}}{\overline{SA}} (avec~ \mathrm{\tan(i)\approx i}}$ dans l’approximation de Gauss)
• Origine aux foyers (Newton) :
  $\mathrm{\overline {FA} \times \overline {F'A'} = \overline {SF} \times \overline {SF'} = f \times f', \gamma =-\frac{f}{\overline{FA}}=\frac{\overline {F'A'}}{f'}}$
  

Formule de Lagrange-Helmholtz :
$\mathrm{n_1 \times \overline{AB} \times \theta = n_2 \times \overline {A'B'} \times \theta '}$

Association de deux systèmes centrés

Il est possible d’associer deux systèmes centrés. Dans ce cas, le système devient afocal si l’intervalle optique $\mathrm{\Delta}$ est nul. On note $\mathrm{\Delta =\overline{F_1' F_2}}$

Dans ce cas :

• le grandissement linéaire est donné par $\mathrm{\gamma =\frac{f_2}{f'_1}}$
• le grandissement angulaire $\mathrm{g=\gamma ^2 \frac{n_2}{n_1}}$

Le système afocal permet donc d’observer des objets à très grande distance (télescopes).

Lentilles minces, lentilles épaisses

Une lentille est une association de deux dioptres sphériques définis par les distances algébriques de leurs sommets à leurs centres respectifs. Dans le cas d’une lentille mince, l’épaisseur au niveau du centre optique est faible devant celle de $\mathrm{R_1=\overline{S_1 C_1}}$, $\mathrm{R_2=\overline{S_2 C_2}}$ et $\mathrm{|\overline{R_1-R_2}|}$

Les lentilles épaisses :

Les lentilles minces :

Le centre optique O est un point de l’axe optique tel qu’un rayon incident quelconque est parallèle à son rayon émergent.

Dans le cas d’une lentille mince, les plans principaux sont confondus.

Un système centré est un enchaînement de plusieurs dioptres et/ou miroirs présentant une symétrie de rotation autour d’un axe optique principal.
Si le système ne contient que des dioptres, il est dioptrique. S’il contient au moins un miroir, il est catadioptrique.
Il existe les systèmes focaux présentant des foyers objet et image à distances finies et des systèmes afocaux avec des foyers rejetés à l’infini.
Un système centré est entièrement défini lorsqu’un couple de points cardinaux (points remarquables) et une distance focale ou deux couples de points cardinaux sont connus.

Le système centré est caractérisé par ses :

• plans principaux, conjugués et présentant un grandissement $\mathrm{\gamma = +1}$. Ils seront notés $\mathrm{[H]}$ et $\mathrm{[H']}$
• plans focaux, plans de front passant respectivement par les foyers principal objet $\mathrm{F}$ et principal image $\mathrm{F'}$
• foyers secondaires, situés à l’intersection du plan de front passant par $\mathrm{F}$ et du rayon issu de $\mathrm{F'}$ ayant son objet à l’infini
• distances focales $\mathrm{f=\overline{HF}~et~f'=\overline{H'F'}}$ sa vergence $\mathrm{V=\frac{n'}{f'}=-\frac{n}{f}}$, positive pour les systèmes convergents et négative pour les systèmes divergents
• ses points nodaux $\mathrm{N}$ et $\mathrm{N'}$ (conjugués), appartenant à l’axe optique, tel que le rayon incident est parallèle au rayon émergent. $\mathrm{\overline{HN}=f+f'}$, tel que si $\mathrm{n_1 = n_2}$, alors les points nodaux sont situés sur $\mathrm{[H]}$ et $\mathrm{[H']}$

Les relations de conjugaison deviennent alors :

• Origine aux points principaux :
  $\mathrm{\frac{f}{\overline{HA}} +\frac{f'}{\overline{H'A'}} =1}$
• Origine aux foyers (Newton) :
  $\mathrm{\overline{FA} \times \overline{F'A'}=f \times f'}$
• Grandissement :
  $\mathrm{\gamma =-\frac{f}{\overline {FA}} = -\frac{\overline {F'A'}}{f'}}$
  

Les instruments d’optique sont classés en :

• instruments objectifs, qui ne nécessitent pas la présence de l’œil humain et dont l’image peut être projetée (caméra, projecteur)
• instruments subjectifs, qui nécessitent la présence de l’œil pour observer l’image (loupe, microscope, verres correctifs, …)

Leur qualité dépend :

• de leur focométrie : formation d’une image correcte par focalisation des rayons lumineux
• de leur photométrie : capacité à transporter un flux et une énergie
• de leur capacité à corriger les aberrations
• de la prise en compte des défauts de l’œil (pouvoir séparateur, acuité, défauts visuels)
• de leurs solutions techniques (diaphragmes de champ ou d’ouverture)
• de leur prise en compte de l’optique physique (aspect ondulatoire et corpusculaire de la lumière)

Ils sont caractérisés par leur :

• Grandissement : rapport entre la taille de l’image et celle de l’objet $\mathrm{\gamma = \frac{A'B'}{AB}}$
• Puissance : quand un objet réel donne une image virtuelle à distance finie, $\mathrm{P=\frac{\alpha'}{AB}}$ avec $\mathrm{\alpha’}$ en radians et $\mathrm{P}$ en dioptries, et la puissance intrinsèque $\mathrm{P_i=\frac{1}{f}}$
• Grossissement : 
• quand l’objet est à l’infini ou très éloigné et lorsque l’image est virtuelle $\mathrm{G=\frac{\alpha'}{\alpha}}$ ($\mathrm{\alpha}$ étant l’angle sous lequel l’objet est vu à l’œil nu à la distance minimale de vision distincte $\mathrm{d}$)
• quand l’objet est proche et lorsque l’image est virtuelle, on parle de grossissement conventionnel $\mathrm{G=\frac{\alpha'}{\alpha}=P \times d}$ 
• le grossissement commercial est défini pour $\mathrm{d=0,25~m : G_c=\frac{P}{4}}$
  

Les instruments optiques sont également caractérisés par leur champ transversal. Le faisceau utile est issu du point A et atteint le point A’ après un système  centré et un certain nombre de diaphragmes afin d’améliorer le stigmatisme.

On distinguera :

• La pupille d’entrée : le diaphragme d’ouverture Do. Le faisceau lumineux issu du champ de pleine lumière ne sera pas vignetté par la pupille d’entrée. Un point hors de ce champ le sera totalement ou en partie et son éclairement (appareil objectif) ou sa luminance (appareil subjectif) décroîtra. On l’appellera également cercle oculaire. D’où l’intérêt d’y placer l’œil directement afin de recevoir le maximum de flux lumineux.
• La lucarne : le diaphragme limitant au maximum l’ouverture utile du faisceau. Le champ de contour passe par les extrémités de la lucarne. Au-delà de ce champ, plus aucune lumière ne passe.
  

Une grandeur spectrale dépend de sa longueur d’onde, à savoir la distance en mètres nécessaire à la répétition d’un motif élémentaire. On donne $\mathrm{\lambda_0=\frac{c}{ν}=c \times T}$ avec :

• $\mathrm{\lambda_0}$ la longueur d’onde en mètres
• $\mathrm{c}$ la célérité de la lumière en $\mathrm{m.s^{-1}}$
• $\mathrm{v}$ la fréquence de l’onde en $\mathrm{Hz}$

Un objet peut être soit une source primaire, responsable de l’éclairement (étoile, lampe) ou une source secondaire, diffusant la lumière issue d’une autre source primaire (table, chaise, …)

La lumière blanche présente un spectre continu entre $400$ et $\mathrm{800~nm}$. Toutes les longueurs d’ondes sont émises. Cependant, il existe des dispositifs ne présentant qu’une ou plusieurs « raies » d’émission. Ce sont des spectres discontinus, caractéristiques des éléments utilisés.

• lampe à sodium (monochromatique) : $1$ raie à $\mathrm{590~nm}$
• lampe à mercure (polychromatique) : $7$ raies principales à $\mathrm{405~nm, 436~nm, 546~nm, 577~nm, 579~nm, 580~nm, 615~nm}$

En termes de sensibilité spectrale, l’œil humain capte mieux les longueurs d’ondes de $\mathrm{555~nm}$ (vert) en vision diurne et $\mathrm{507~nm}$ (bleu) en vision nocturne.

Pour caractériser la lumière, on utilise les grandeurs suivantes :

• $\mathrm{\Delta \Phi}$, le flux (lm, W) : c’est le débit de lumière le long d’un rayon
• $\mathrm{I}$, intensité $\mathrm{(cd, W.sr^{-1})}$  : c’est le flux de lumière émis par unité d’angle solide $\mathrm{\Omega}$

$\mathrm{\displaystyle I=\frac{\Phi_{émis}}{\Omega}}$ et $\mathrm{\Omega =\frac{S \times \cos \alpha}{d^2}}$

• $\mathrm{L}$, luminance $\mathrm{(cd.m^{-2}, W.sr^{-1}.m^{-2})}$ : c’est l’intensité lumineuse émise par unité de surface apparente de la source.
• $\mathrm{E}$, éclairement $\mathrm{(lux, W.m^{-2})}$ : c’est le flux reçu par unité de surface

$\mathrm{E=\frac{\Phi_{émis}}{S}}$ et $\mathrm{E=\frac{I \times \cos\alpha}{d^2}}$

Le collecteur de flux doit permettre de capter tout le flux issu de la source sans en reconstituer une géométrie parfaite. Un capteur d’image doit au contraire reconstituer la géométrie d’une image.

On distingue 2 types d’aberrations :

• Les aberrations chromatiques, persistantes dans les conditions de Gauss
• Les aberrations géométriques, absentes dans les conditions de Gauss

Les aberrations chromatiques

Chaque longueur d’onde se réfractant à des angles légèrement différents (cas de l’arc en ciel), les foyers images de chaque couleur peuvent être différents.
Le nombre d’Abbe correspond à l’inverse du pouvoir dispersif d’un système optique. Avec le nombre d’Abbe $\mathrm{ν=\frac{n_D -1}{n_F-n_C}}$ avec $\mathrm{n_D}$ l’indice de réfraction pour la raie jaune du sodium, $\mathrm{n_F}$ pour la radiation bleue de l’hydrogène, $\mathrm{n_C}$ pour la radiation rouge de l’hydrogène et la focale, il est possible de prévoir l’aberration chromatique.
L’aberration chromatique longitudinale est proportionnelle à la distance focale moyenne :

$\mathrm{\displaystyle \frac{\Delta f'}{f'_{moyen}} = \frac{1}{ν}}$

Chaque matériau se comporte différemment. La formule de Cauchy permet de représenter le pouvoir dispersif d’un matériau (A, B déterminés expérimentalement) en fonction de la longueur d’onde considérée :

$\mathrm{n(\lambda)=\frac{A+B}{\lambda^2}}$ 

Les aberrations géométriques :

Quelques exemples : les aberrations de coma, les aberrations sphérique, la courbure de champ.

La propagation de la lumière est un phénomène vibratoire, modélisé par :

$\mathrm{S_1=A_1 \cos⁡ (\omega t-\varphi_1)}$
$\mathrm{S_2=A_2 \cos⁡ (\omega t-\varphi_2)}$

Avec $\mathrm{I_1=A_1^2}$ et $\mathrm{I_2=A_2^2}$, pour 2 signaux ayant la même longueur d’onde et la même pulsation $\mathrm{\omega}$. 

L’intensité du signal résultant est donc :

• $\mathrm{I=I_1+I_2+2 \sqrt{I_1 I_2} \cos⁡(\varphi)}$, avec :
• $\mathrm{2\sqrt{I_1 I_2} \cos⁡(\varphi)}$ représentant le terme d’interférence
• $\mathrm{\varphi =\varphi_1-\varphi_2=2\pi \frac{\delta}{\lambda_0}}$ 

Le terme d’interférence est donc maximal pour $\mathrm{\delta=k \times \lambda_0}$ (l’interférence est constructive) et minimal pour $\mathrm{\delta=(k+\frac{1}{2}) \times \lambda_0}$ (l’interférence est destructive), à condition que les ondes soient cohérentes (même pulsation et même direction).

Interférences dans une lame parallèle

Chaque frange produite possède la même intensité.

La différence de marche est :

• Pour la transmission :
  $\mathrm{\delta =[BC]+[CD]-[BH'] =2 \times n_1 \times e \times \cos⁡(r)}$
• Pour la réflexion :
  $\mathrm{\delta =[AB]+[BC]-[AH]=2 \times n_1 \times e \times \cos⁡(r)+ \frac{\lambda_0}{2}}$
  (les 2 rayons sont de nature différente)

La figure d’interférence forme donc des cercles concentriques de centre F’, avec des interférences constructives en transmission pour des interférences destructives en réflexion et inversement.

Interférences dans un coin d’air

Si $\mathrm{\alpha}$ est très petit, alors on observe des franges d’interférences pour une réflexion (meilleur contraste).

Interférences, anneaux de Newton

Pour obtenir des anneaux de Newton, il faut utiliser une lentille plan convexe, en contact avec une lame de verre.

Traitement anti-réfléchissant des surfaces

On appose un matériau transparent d’indice $\mathrm{n_2}$ de façon à générer des interférences destructrices en réflexion. Dans le cas d’une incidence normale, on a alors :

$\mathrm{\delta = 2 \times n_1 \times e}$ et $\mathrm{\delta = (k+\frac{1}{2})\lambda_0}$

• Les intensités des deux premiers rayons réfléchis sont $\mathrm{I_1=I_R \times I_0~et ~I_2=I_{R2} \times I_T^2 \times I_0}$
• Les valeurs possibles de $\mathrm{e}$ sont $\mathrm{\displaystyle e=\frac{(k+\frac{1}{2})λ_0}{2n}}$
• L’indice idéal de la couche antireflet est $\mathrm{n_1=\sqrt{n_2}}$.

La lumière naturelle n’est pas polarisée : ses vibrations suivent toutes les directions possibles. Il est possible de la polariser linéairement dans une direction privilégiée grâce à un filtre polariseur.

Si on ajoute un 2ème polariseur après un premier $\mathrm{(P)}$, il se nommera « analyseur » $\mathrm{(A)}$ et permettra de contrôler l’intensité du faisceau émergent. La loi de Malus nous donne l’intensité finale :

$\mathrm{I_A=I_P \times \cos^2 \alpha, avec ~{I_P=\frac{I_0}{2}}}$

Quand la lumière est réfléchie face à un dioptre séparant 2 milieux d’indices respectifs $\mathrm{n_1}$ et $\mathrm{n_2}$ , elle est polarisée rectilignement, dans une direction perpendiculaire au plan d’incidence, à condition que le rayon transmis et le rayon réfléchis soient eux-mêmes perpendiculaires. On a donc :

$\mathrm{i_b + i_t = 90°}$. 

En injectant cette condition dans la 2ème loi de Descartes, on obtient la loi de Brewster :

$\mathrm{\tan⁡i_b=\frac{n_2}{n_1}}$

Il existe un cas de bi réfringence où un cristal est capable de dédoubler les faisceaux lumineux. Il se produit alors :

• un rayon ordinaire, issu de la réfraction normale, polarisée rectilignement $\mathrm{(R_0, n_0)}$
• un rayon extraordinaire, issu d’une réfraction anormale d’indice variable entre $\mathrm{n_0}$ et ne, polarisée rectilignement, de direction perpendiculaire à celle du rayon ordinaire.

Comme l’indice $\mathrm{n}$ dépend de la direction de polarisation, un tel cristal est anisotrope.

La diffraction est un phénomène inévitable qui produit des limites non nettes des images. Il a l’inconvénient de limiter la résolution des instruments optiques, mais l’avantage de décomposer les spectres lumineux.

Lorsqu’un faisceau lumineux rencontre un obstacle, il ne suit plus une propagation rectiligne, mais suit le principe d’Huygens – Fresnel, selon lequel la lumière se propage en formant une nouvelle onde sphérique au point suivant. L’onde suit alors les différentes interférences produites entre toutes ces ondes.

Diffraction par une ouverture circulaire

Quand un faisceau traverse un diaphragme de diamètre d, on obtient une figure de diffraction constituée d’une tache centrale très lumineuse, appelée tache d’Airy de rayon $\mathrm{\rho}$, encerclée de différents cercles concentriques.

La tache d’Airy est d’autant plus grande que 

• $\mathrm{d}$ est petit
• $\mathrm{\lambda}$ est grande

Diffraction par une fente fine

Lorsque l’obstacle est une fente fine, la tache centrale est beaucoup plus lumineuse. On remarque sur le graphique d’intensité que la frange centrale est deux fois plus large que les taches diffractées, et que les minima d’intensité se situent à $\mathrm{\sin \theta = \frac{m\lambda}{D}}$ avec m un entier relatif non nul.

Diffraction par un réseau par transmission

La différence de marche est dans ce cas :

$\mathrm{\delta = S_2 H_2 – H_1 S_1 = a \times (\sin⁡(i')-\sin⁡(i))=k \times \lambda_0}$

avec $\mathrm{k}$ un entier relatif (on a choisi $\mathrm{\delta = k \times \lambda_0}$ pour obtenir les maxima principaux grâce à des interférences constructives.

A $\mathrm{k=0}$, on obtient un rayon non dévié avec un maximum d’intensité lumineuse pour $\mathrm{i=i'}$.

Pouvoir séparateur

Deux images sont séparées l’une de l’autre à condition qu’une tache d’Airy corresponde au premier minimum de l’autre. Dans ce cas, l’instrument possède un bon pouvoir séparateur. Le pouvoir séparateur est inversement proportionnel à la limite de résolution.

Le pouvoir de résolution détermine la distance à laquelle deux points sont distincts. Il dépend en partie du phénomène de diffraction, mais aussi de la taille des grains d’une émulsion pour un négatif photographique ou la définition du capteur pour un capteur photo numérique.

L’ouverture, la distance de mise au point et la longueur focale permettent de calculer la profondeur de champ et déterminer les zones floues et nettes.

La limite de résolution œil-instrument se résout à étudier le phénomène de diffraction de l’instrument d’une part, et la limite du capteur due à la taille des pixels ou des grains argentiques et à prendre la plus grande résolution des deux.