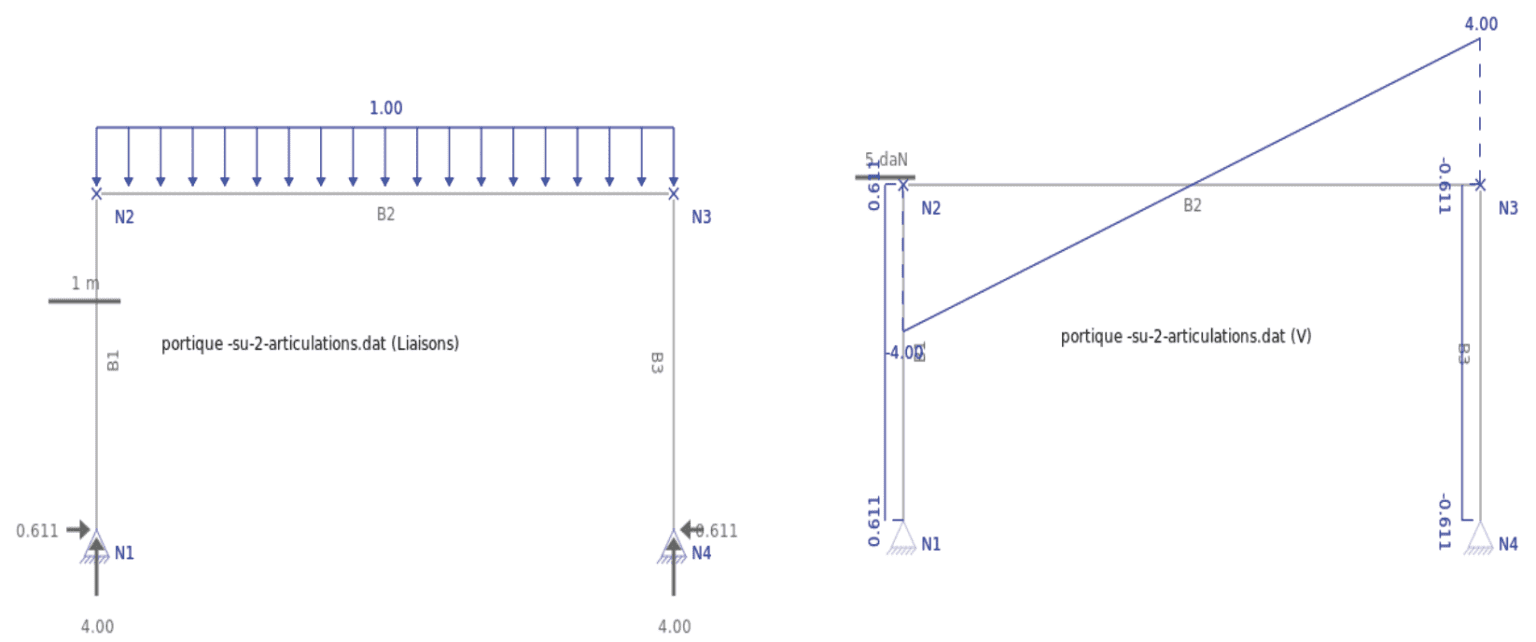
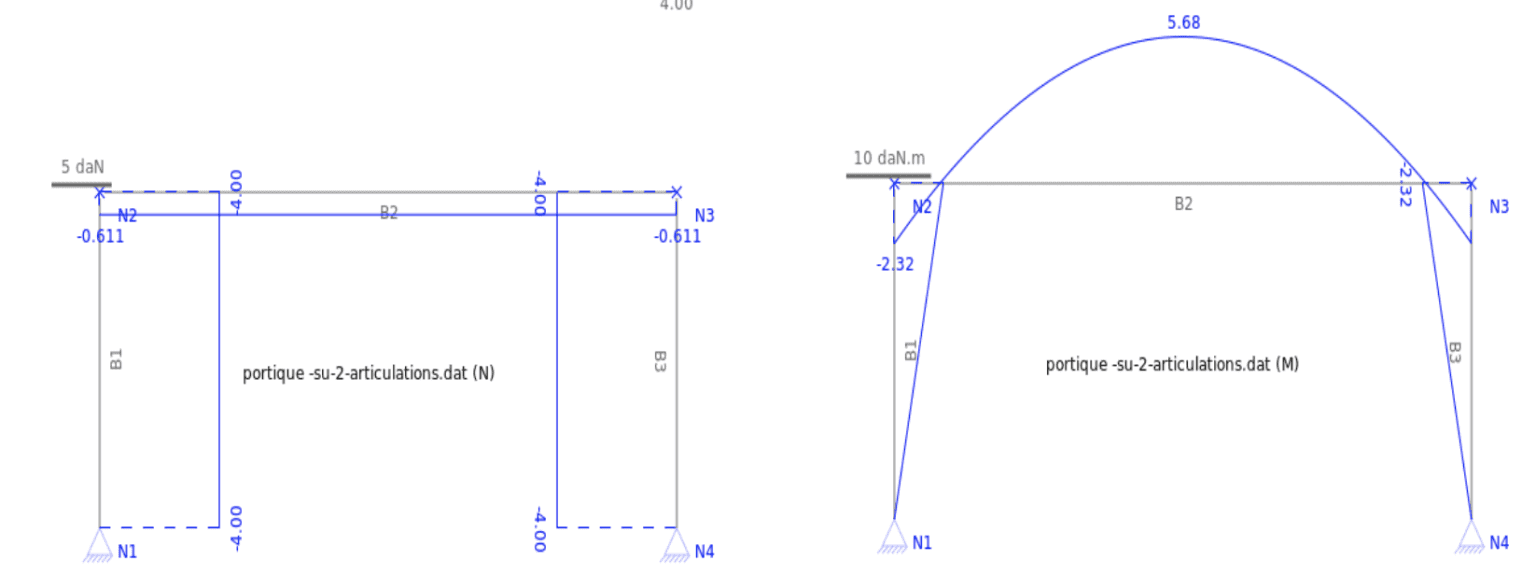
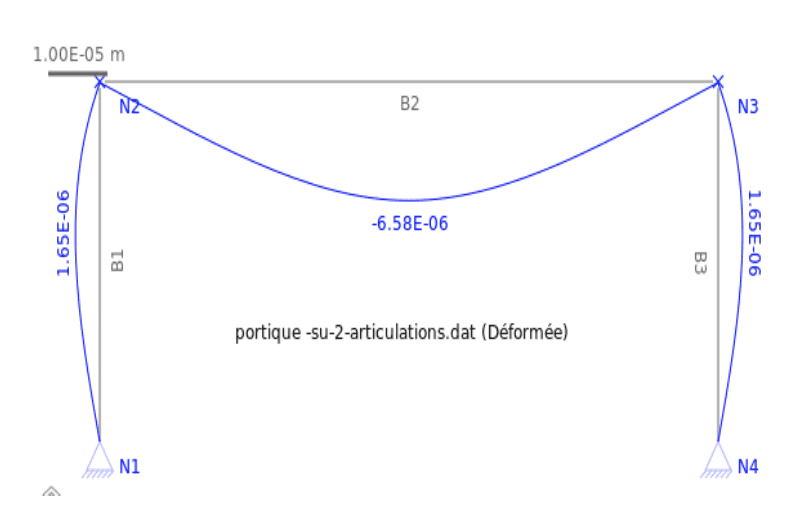
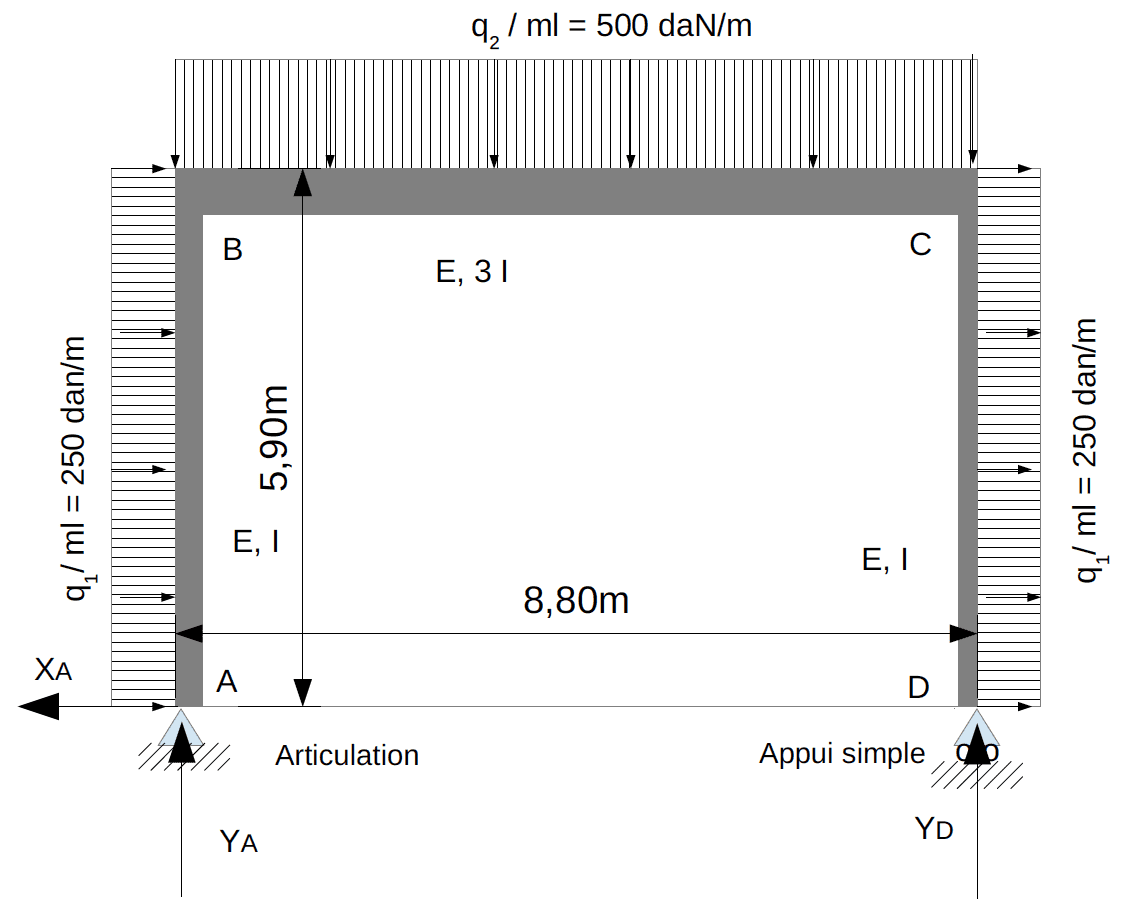
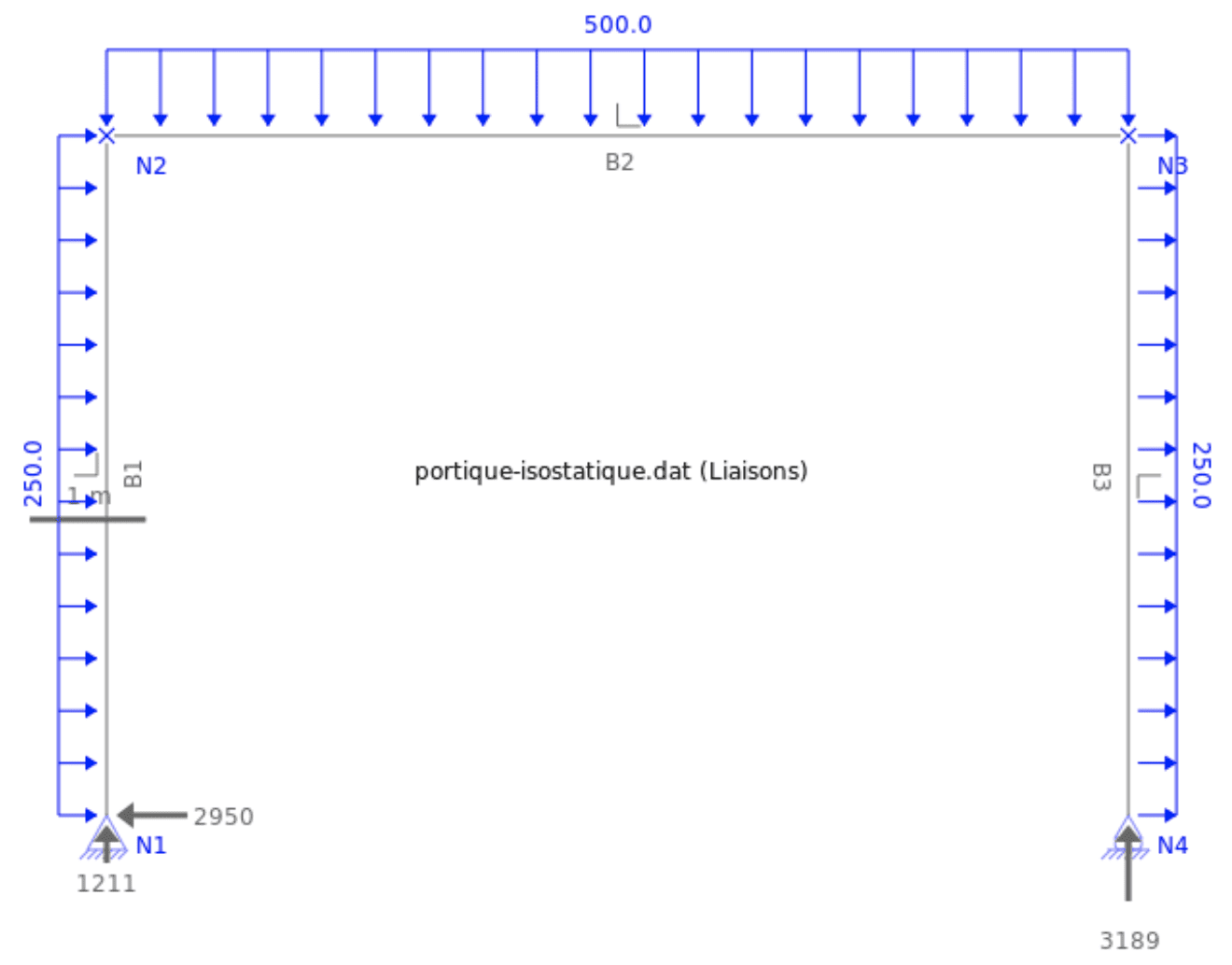
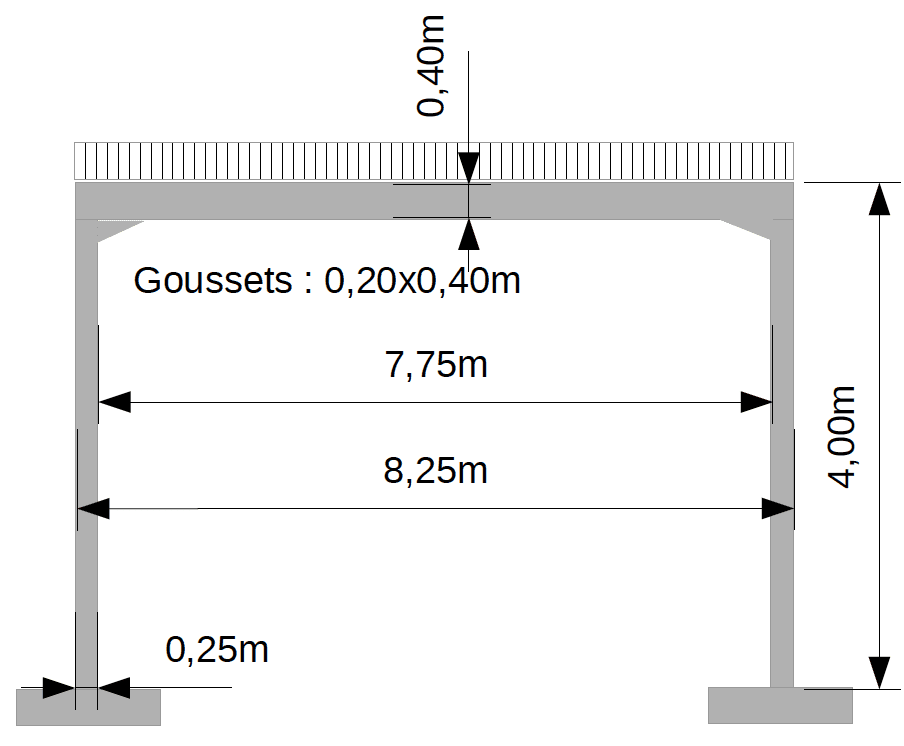
Schéma mécanique associé :
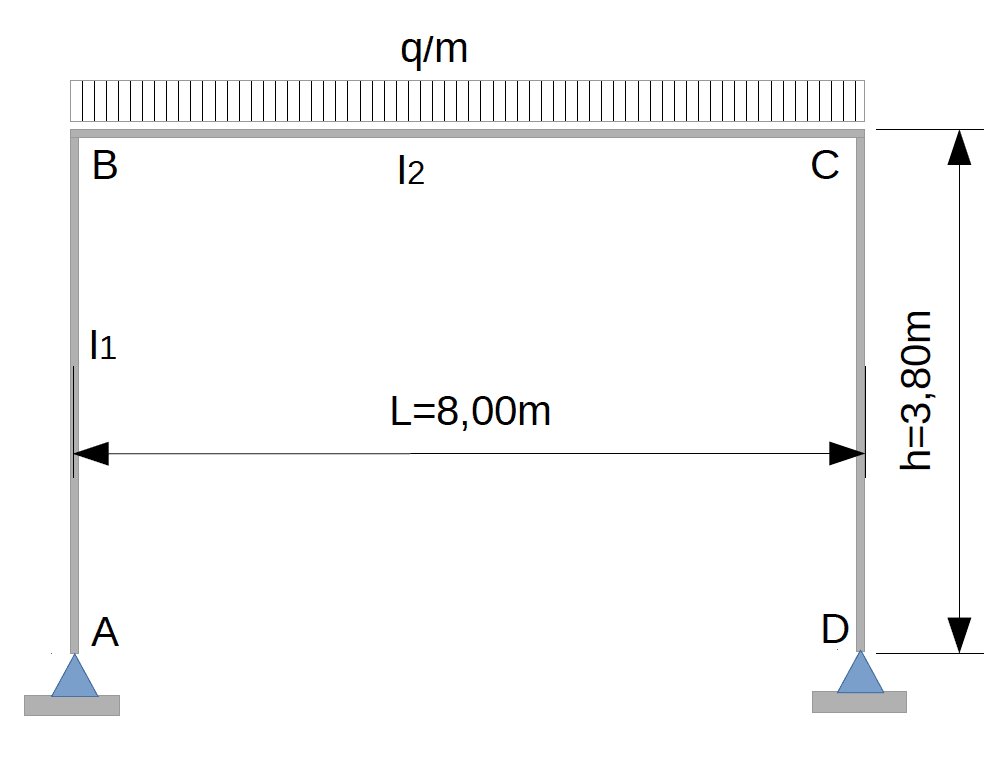
Les dimensions sont ramenées aux axes des poteaux et de la poutre.
Bilan réel du chargement sur la poutre :
$\rm G=450~daN/m$ ; $\rm Q=150~daN/m$
Coefficient de corrélation avec le schéma mécanique (de façon à ce que les actions verticales en $\rm A$ et $\rm D$ donnent la même somme que la charge répartie en $\rm BC$) :
$\rm \dfrac{8,25}{8,00} = 1,032$
$\rm \Rightarrow G=465~daN/m$ ; $\rm Q=155~daN/m$
$q_{\rm ELS} = 620~\rm daN/m$
$q_{\rm ELU} = \rm 861~daN/m$
Inconnues de liaison :
$\rm X_AY_A$ ; $\rm X_D Y_D \Rightarrow 4~inconnues$
$d=\rm I−E=4−3=1 \Rightarrow \text{ hyperstatique d'ordre 1}$
Les qualités de symétrie du portique nous permettent d’affirmer :
$\rm Y_A = Y_D$ $=\dfrac{ql}{2}$ ; $\rm X_A~(\rightarrow) = X_D~ (\leftarrow)$
Calcul des actions mécaniques horizontales par la méthode des forces.
On décompose en deux systèmes isostatiques.
On libère l’articulation $\rm D$ pour la transformer en un appui simple pouvant se déplacer horizontalement. Le déplacement associé se nommera $\Delta 10$.
On associe un $\rm 2^{ème}$ système avec une force unité en $\rm A$ et $\rm D$.
Le déplacement en $\rm D$ associé se nommera $\delta_{11}$
$\rm X_1$ sera l’inconnue liée au déplacement horizontal de l’appui simple $\rm D$.
L’ensemble ne doit pas avoir de déplacement (articulation), d’où :
$\Delta_{10} + X_1\delta_{11}=0$ $\rm\Rightarrow X_1 =−\Delta_{10} \delta_{11}$ $\rm = X_A = X_D$
$\displaystyle \rm\Delta_{10} = \dfrac{1}{EI_1}\int_0^h M \overline M \mathcal{dy}$ $+$ $\displaystyle \rm\dfrac{1}{EI_2} \int_0^L M \overline M \mathcal{dx}$ $+$ $\displaystyle \rm\dfrac{1}{EI_1} \int_0^h M \overline M \mathcal{dy}$ $\displaystyle \rm= \dfrac{1}{EI_2} \int_0^L M \overline M \cal dx$ car $\rm M=0$ pour les poteaux $\displaystyle \Delta_{10} = \dfrac{1}{\rm EI_2} \int_0^{\rm L} \left[\dfrac{−qx^2}{2} + \dfrac{q\mathrm Lx}{2}\right][−h]dx$ $\displaystyle =\dfrac{−h\rm q}{2 \rm EI_2} \int_0^{\rm L} \left[−x^2 + \mathrm Lx\right]dx$ $=\dfrac{−q\rm hL^3}{12 \rm EI_2}$
$\rm\displaystyle \delta_{11} = \dfrac{1}{EI_1} \int_0^h (−\mathcal y)^2 \mathcal{dy}$ $+$ $\rm\displaystyle \dfrac{1}{EI_2} \int_0^L (−h)(−h)\mathcal{dx}$ $+$ $\rm\displaystyle \dfrac{1}{EI_1} \int_0^h \left[−(h−\mathcal y)^2\right]\cal dy$ $\rm =\dfrac{h^2}{3 E} \left[2\dfrac{h}{I_1} + \dfrac{3L}{I_2}\right]$
$\rm \Rightarrow X_1 = \dfrac{−\Delta_{10}}{\delta_{11}} = \dfrac{\mathcal qL^3 I_1}{4h[2hI_2 + 3LI_1]}$
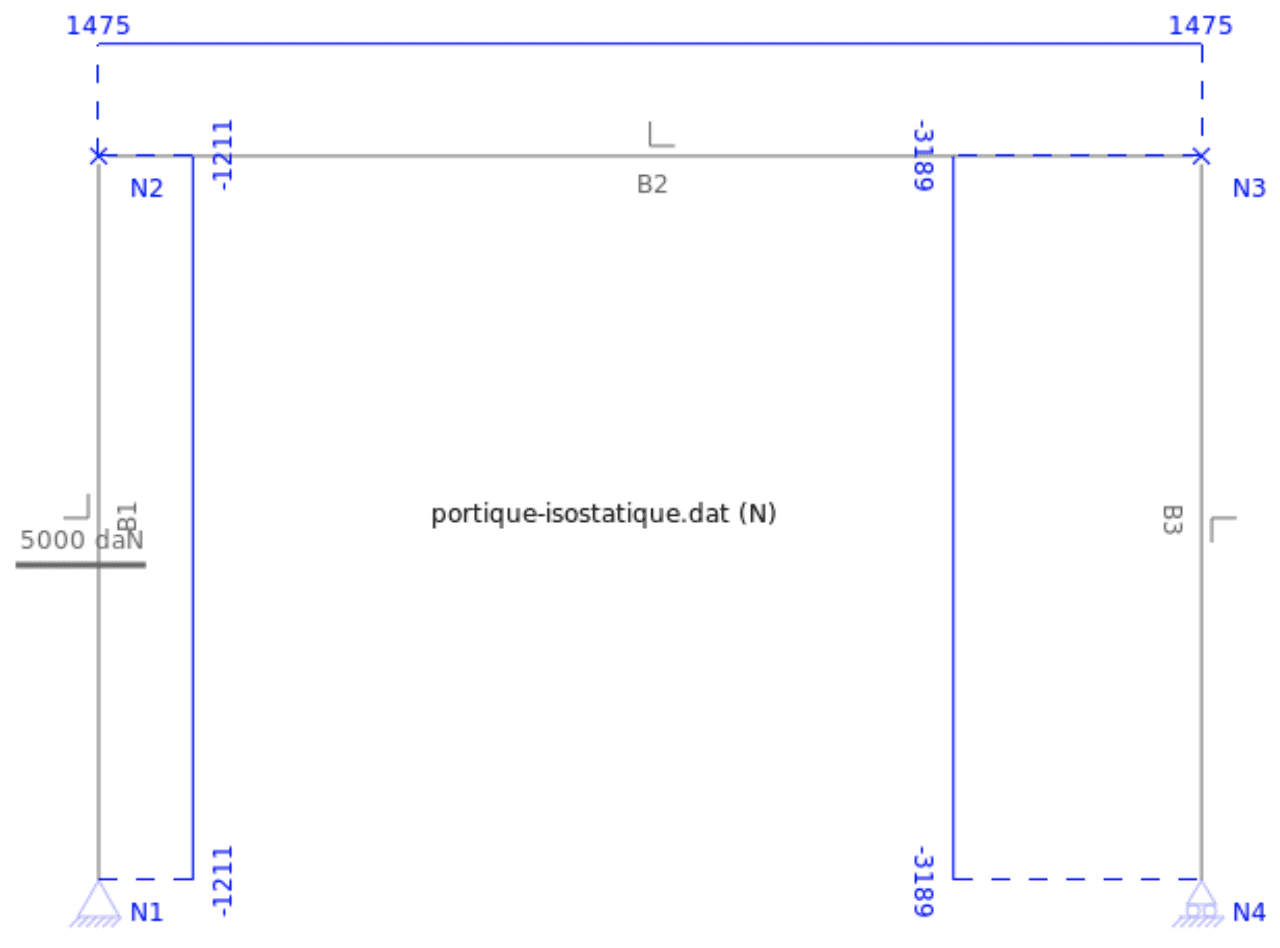
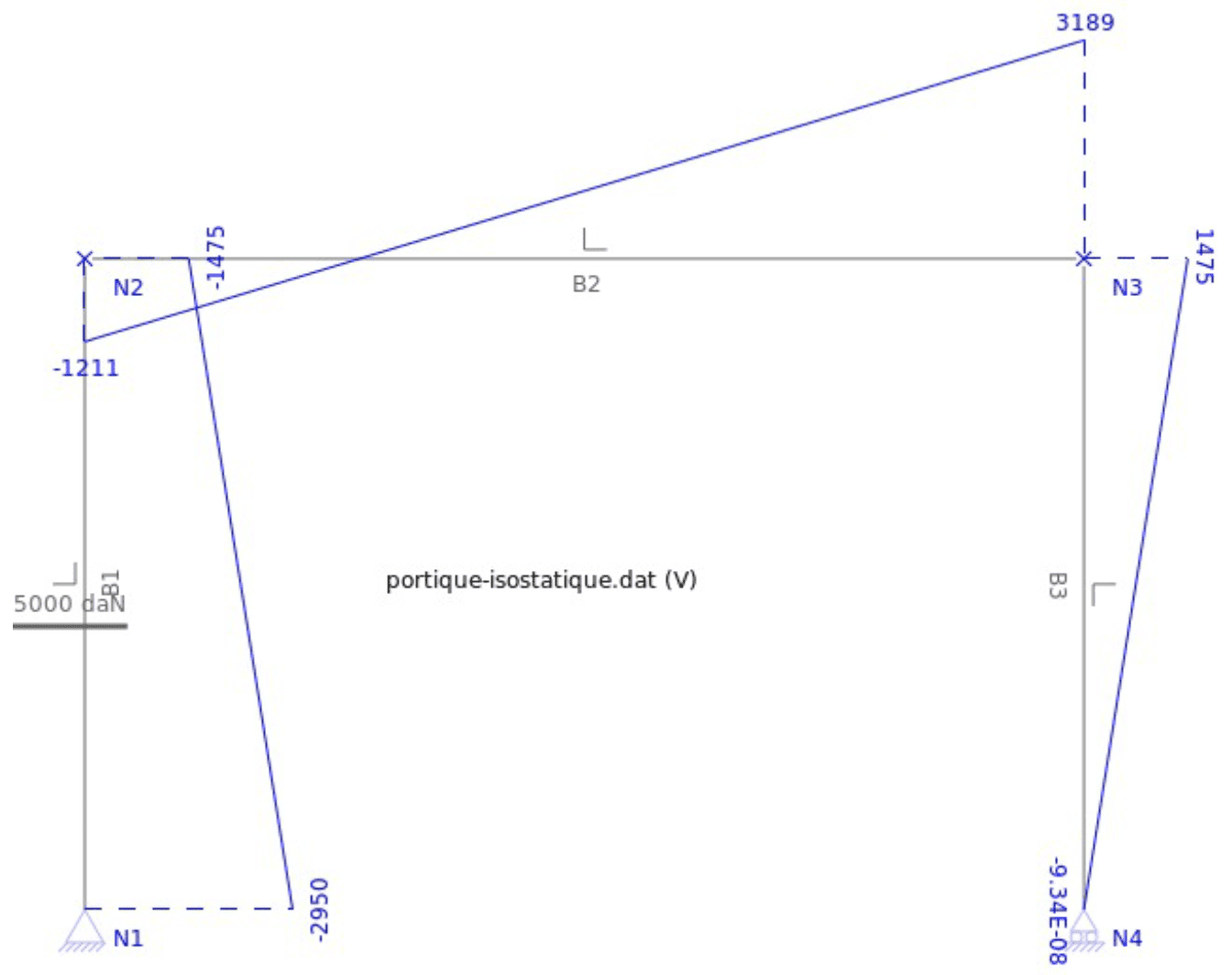
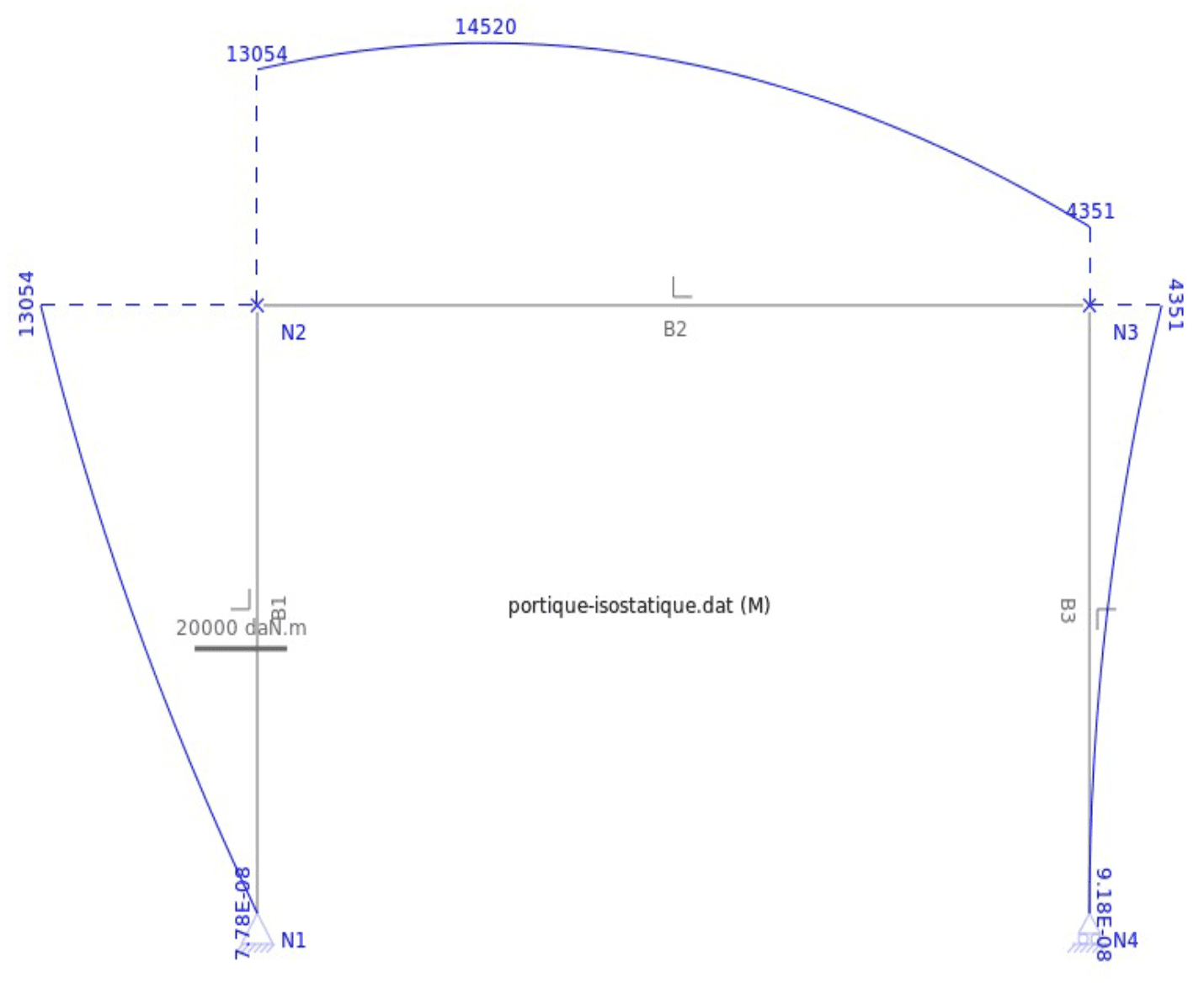
En supposant les matériaux homogènes, on peut calculer les moments quadratiques $\rm I_1$ et $\rm I_2$ : Les diagrammes de $\rm N$, $\rm V$, $\rm M$ et déplacements, sont ci-après. On remarquera que les actions horizontales $\rm X_A$ et $\rm X_D$ dépendent des grandeurs géométriques du portique et notamment pour beaucoup aux moments quadratiques.