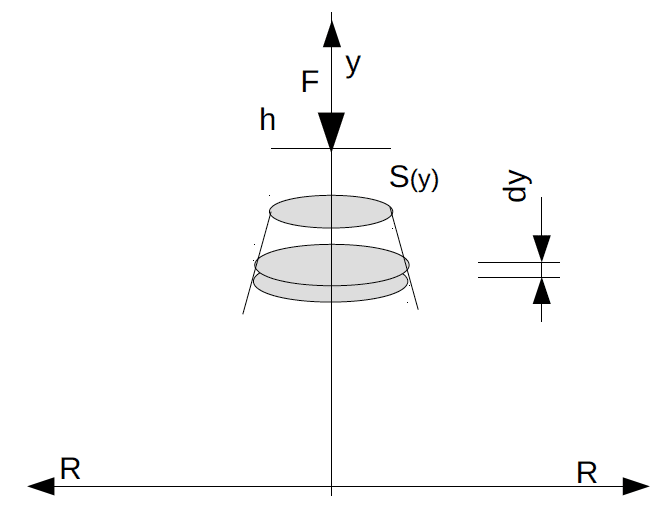
Les déformations dans les poteaux sont liées à deux phénomènes :
- Déformation par compression simple, liée à des forces bien placées dans l’axe du poteau, dont la section est supposée parfaitement symétrique.
- Déformation liée à phénomène du second ordre, appelé flambage ou flambement, qui tient compte du fait que le poteau est très élancé et a des formes imparfaites.
On commencera par les poteaux bi-articulés, donc sans déplacement latéral en tête et en pieds (figure ci-dessous). On suppose que la liaison supérieure peut suivre le mouvement d’affaissement.
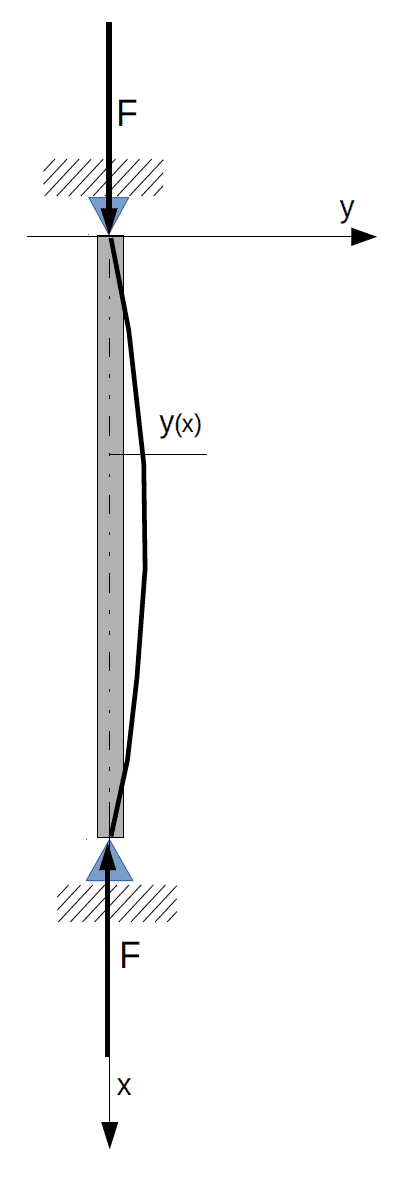
M(x)=−Fy(x) ⇒EIy″(x)+Fy(x)=0 ⇒y″(x)+FEIy(x)=0
α2=FEI⇒y″(x)+α2y(x)=0
C’est une équation différentielle du 2ème ordre sans second membre dont la solution peut se mettre sous la forme d’une exponentielle complexe ou sous la forme d’une combinaison de sinus et cosinus (voir rappels de mathématiques).
y(x)=Asin(αx)+Bcos(αx)
Conditions aux limites :
x=0⇒y(x=0)=0⇒B=0
x=l⇒y(x=l)=0⇒Asin(αl)=0
⇒ soit A=0 sans interêt ou soit sin(αl)=0⇒α=kπl
Il y a une infinité de solutions, mais la nature préfère la solution la plus simple, soit :
k=1⇒α=πl=√FEI
FEI=π2l2 ⇒F=π2EIl2 → Force critique d'Euler.Rayon de giration r=√IS ; élancement λ=lcr lc= longueur de flambement =l ⇒σc=π2Eλ2 → Contrainte critique d'Euler liée au flambement.
Pour qu’un poteau résiste correctement à un effort vertical centré, il faudra vérifier deux contraintes :
σ≤σc=π2Eλ2 (flambement) et σ≤¯σ → contrainte admissible.
Exemple :
Poteau en acier S235, de section creuse 100×200 mm réalisé avec une tôle de 4 mm. La hauteur est de 5,00 m. Le poteau est bi-articulé. Charge axiale F=25 000 daN =250 kN
Contrainte admissible :
σ=feγs=2351,1=213 Mpa
Contrainte critique d’Euler :
I=20×10312−19,2×9,2312=420,77 cm4 S=20×10−19,2×9,2=23,36 cm2
⇒r=√IS=√420,7723,36=4,244 cm ⇒λ=lcr=5004,244=117,81
σc=π2Eλ2=π2×210 000117,812=149,33 Mpa
σ=FS=0,2523,36⋅10−4 =107,02 Mpa⇒σ<min [σc=149,33 Mpa ; ¯σ=213 Mpa] ⇒OK
Remarque : Le moment quadratique est calculé dans le sens le plus faible.