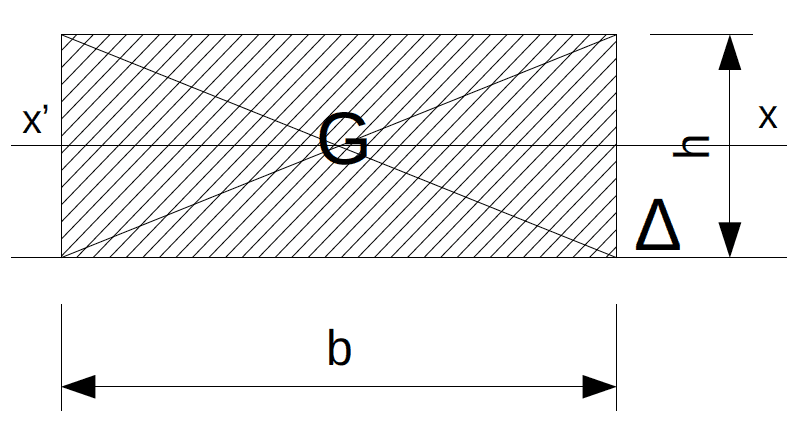
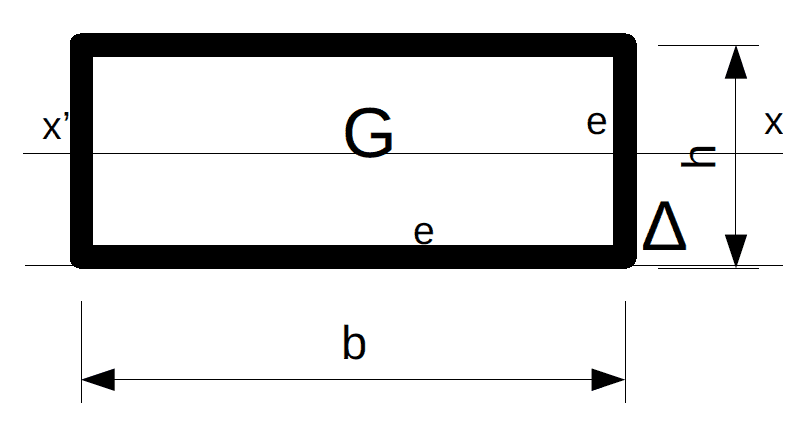
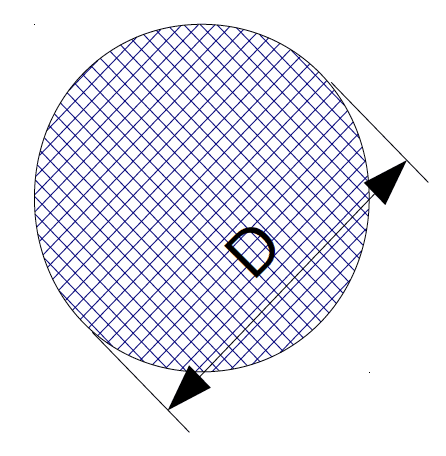
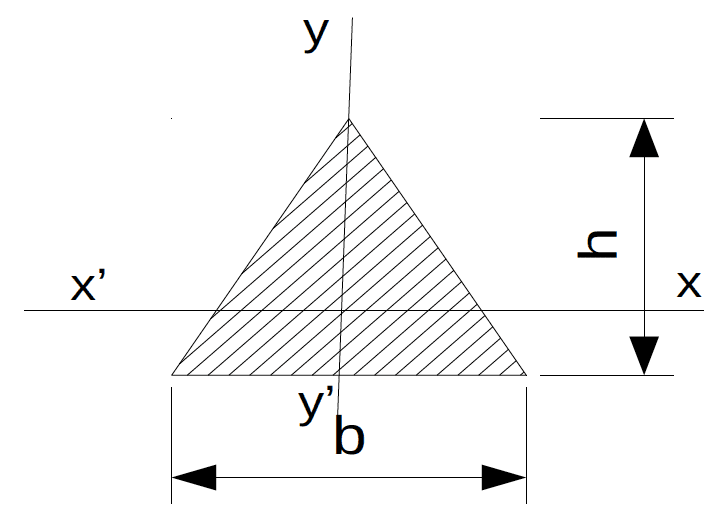Soient trois vecteurs dont on veut faire la somme et le produit scalaire des deux premiers :
→AB=(axayaz) ; →BC=(bxbybz) ; →CD=(cxcycz) ⇒ →AD=(ax+bx+cxay+by+cyaz+bz+cz) et →AB⋅→BC=AB×BC×cos(→AB ;→BC) =(axbx+ayby+azbz)
Dans un plan xoy :
→AB=(axay) ; →BC=(bxby) ; →CD=(cxcy) ⇒ →AD=(ax+bx+cxay+by+cy)
L’unité d’une force est le Newton ou ses multiples.
L’unité de la masse d’un solide est le kg ou ses multiples.
Dans un environnement gravitaire, une masse (kg) génère un poids (N) par la relation :
F=m×γ.
Sur la terre, la valeur moyenne de l’accélération de la pesanteur est :
γ=g=9,81 m/s2.
Application du produit vectoriel, moment d’une force en un point :
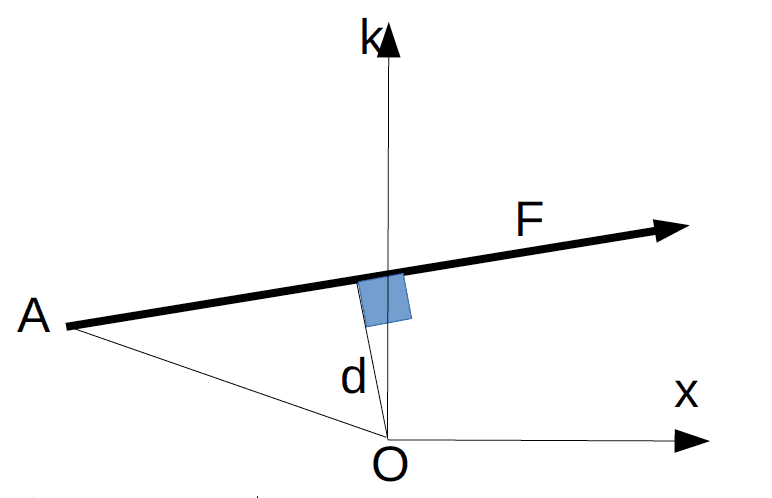
→MoF=→OA∧→F =‖→OA‖×‖→F‖×sin(→OA ;→F) =(axay)∧(Fx ;Fy) =(axFy−ayFx)→k
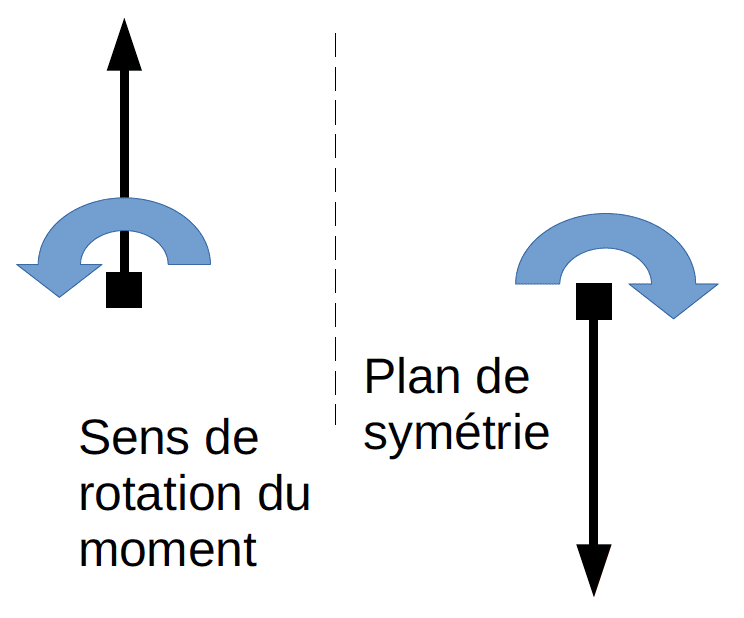
Le symbole ∧ se dit « vectoriel » et définit le produit vectoriel. Le vecteur issu d’un produit vectoriel ne respecte pas les lois de symétrie et donc devient un « pseudo-vecteur » (antisymétrique).
Moment d’une force par le calcul géométrique : →MoF=−d×‖→F‖→k et en appliquant la règle du « tire-bouchon » (ici négatif).
(**) Exemple numérique →F=−500 kN sur y ; d=3,00 m sur x⇒ M/o→F=−1 500 m.kN sur z.
Produit vectoriel dans un système 3D :
→AB=(axayaz) ; →BC=(bxbybz) ; ⇒ →AB∧→BC=(axayaz)∧(bxbybz) =(aybz−byazazbx−bzaxaxby−bxay)
Les indices (x,y,z) ne doivent pas apparaître dans la ligne repérée. Par exemple, la première ligne (axe x) n’a pas d’indice x.
La première ligne (x) est obtenue en faisant les différences des produits croisés des lignes (y) et (z).
Torseur de force et torseur cinématique : ils sont composés d’une résultante et d’un moment résultant. L’écriture symbolique est :
TA=[→R(XYZ)→MA(LMN)] pour le torseur statique écrit au point A (R=force et M un moment résultant).
CA=[→ω(ωxωyωz)→VA(vxvyvz)] pour le torseur cinématique écrit au point A (V=vitesse et ω=vitesse de rotation)
Formules de transfert des moments dans un torseur statique et cinématique :
⇀MA=⇀MB+⇀AB∧⇀R
⇀VA=⇀VB+⇀AB∧⇀ω