Potentiel interne 1

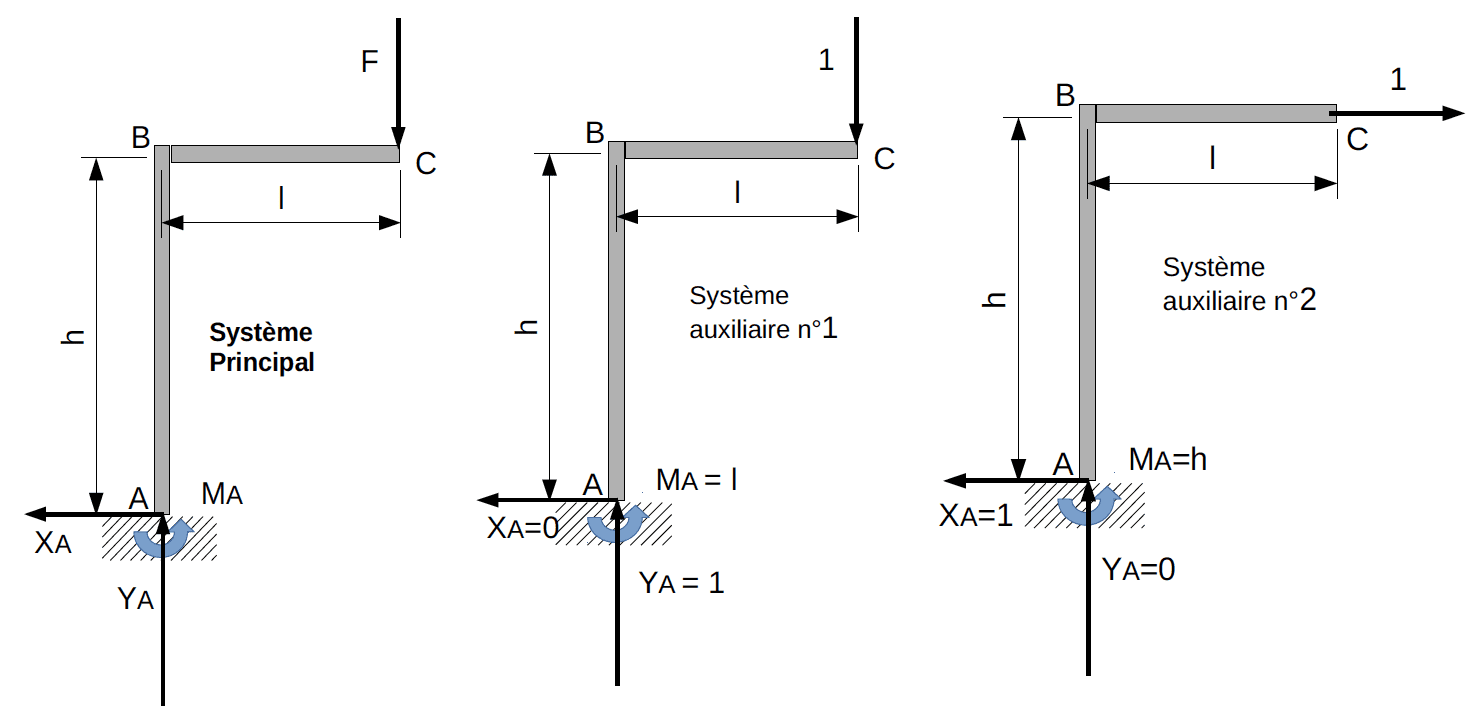
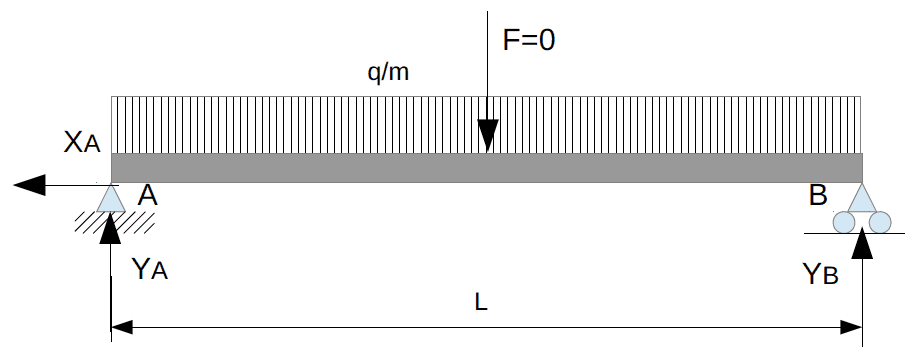
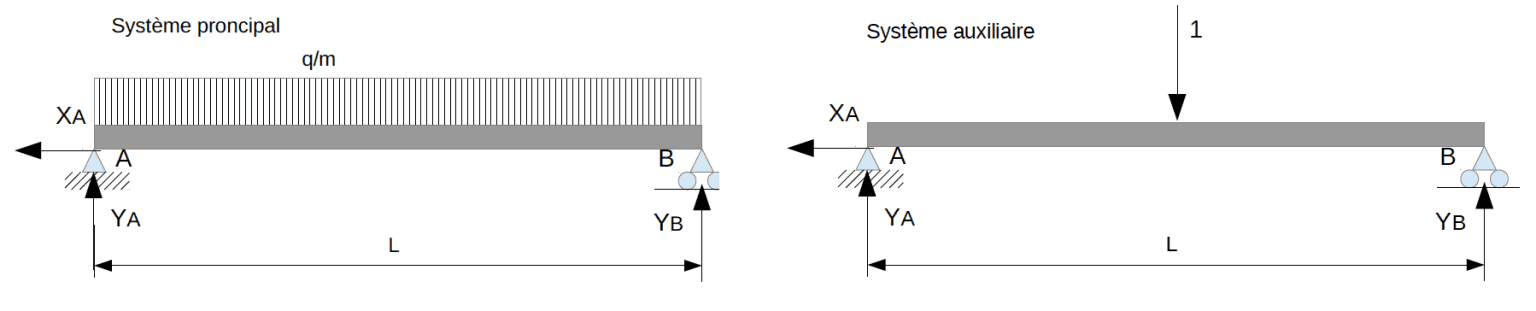
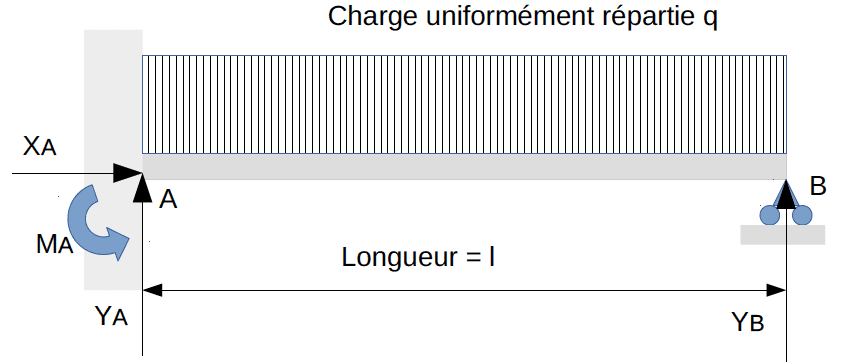
Une poutre soumise à un système de forces $\rm (S)$ se déforme ; pendant le chargement, les points d’application des forces se sont déplacés et les sections d’applications de couples ont tourné. Le système $\rm (S)$ a donc produit un travail $\rm (T)$.
Le travail $\rm (T)$ est donc emmagasiné par la poutre sous forme d’énergie potentielle, nommée $\rm (W)$. Un travail mécanique correspond au produit d’une force par un déplacement parallèle à la force. On peut l’écrire aussi sous la forme d’un produit scalaire.

Expression du travail en fonction des forces appliquées :

Expression du potentiel interne $\rm (W)$ d’une poutre en fonction des efforts normaux $\rm (N)$, des efforts tranchants $\rm (V)$ et des moments
fléchissants $\rm (M)$ :

$\rm W=\dfrac{1}{2} \left[\dfrac{N_{(\mathcal x)}^2}{ES} + \dfrac{V_{(\mathcal x)}^2}{GS_1} + \dfrac{M_{(\mathcal x)}^2}{EI}\right]\cal ds$

Avec :

• $\rm E =$ module d’élasticité longitudinale ou module d’Young.
• $\rm S =$ section totale de la poutre.
• $\rm G =$ module d’élasticité transversale de la poutre.
• $\rm S_1 =$ section spécifique prise en compte pour le cisaillement (pour un profilé en $\rm I$ ou $\rm H$, c’est uniquement l’âme de la poutre).
• $\rm I =$ moment quadratique de la poutre selon l’axe perpendiculaire au plan de la poutre et passant par le $\rm CdG$ de la section.

La dérivée partielle du potentiel interne d’une poutre par l’une des forces du système, donne le déplacement de cette force.
La dérivée partielle du potentiel interne d’une poutre par l’un des couples du système, donne la rotation de ce couple.

$\rm W=\dfrac{1}{2} \left[\dfrac{N_{(\mathcal x)}^2}{ES} + \dfrac{V_{(\mathcal x)}^2}{GS_1} + \dfrac{M_{(\mathcal x)}^2}{EI}\right]\cal ds$ $\Rightarrow$ $\rm \lambda_i =\displaystyle \int_{s_0}^{s_1}$ $\rm \left[\frac{N}{ES} \frac{\partial N_{(\mathcal x)}}{\partial F_i} + \frac{V}{GS_1} \frac{\partial V_{(\mathcal x)}}{\partial F_i} + \frac{M}{EI} \frac{\partial M_{(\mathcal x)}}{\partial F_i}\right]\cal ds$
et
$\varphi_k = \rm\displaystyle \int_{s_0}^{s_1}$ $\rm \left[\frac{N}{ES} \frac{\partial N_{(\mathcal x)}}{\partial C_k} + \frac{V}{GS_1} \frac{\partial V_{(\mathcal x)}}{\partial C_k} + \frac{M}{EI} \frac{\partial M_{(\mathcal x)}}{\partial C_k}\right]\cal ds$

Ces expressions sont aussi appelées « théorème de Ménabréa ».

$ds =$ abscisse curviligne, pouvant être $dx$ si la poutre est horizontale et $dy$ si elle est verticale : Soit un système $\rm (S)$ composé soit d’une force unité, soit d’un couple unité, provoquant les efforts internes $\rm \overline N$, $\rm \overline V$ et $\rm \overline M$.
On constate que les systèmes complémentaires (Force ou couple unité) donnent les mêmes expressions que les dérivées partielles des efforts internes par rapport à $\rm F$ ou $\rm C$.

$\rm \displaystyle \lambda=\int_{s_0}^{s_1} \left[\dfrac{N \overline N}{ES} + \dfrac{V \overline V}{GS_1} + \dfrac{M \overline M}{EI}\right] \cal ds$ ou $\rm \displaystyle \varphi =\int_{s_0}^{s_1} \left[\dfrac{N \overline N}{ES} + \dfrac{V \overline V}{GS_1} + \dfrac{M \overline M}{EI}\right]\cal ds$

L’utilisateur est donc dispensé de calculer les dérivées partielles, mais en contrepartie, il doit formuler les équations des efforts normaux, tranchants et moments fléchissants du système complémentaire unité.

On veut calculer les déplacements horizontaux et verticaux de l’extrémité $\rm C$ de la potence, provoqué par le force $\rm F$ verticale descendante. Voici les deux systèmes auxiliaires correspondant à chacun des déplacements. Déplacement vertical (système auxiliaire n° 1).

Partie AB :

$\rm N=−F$ ; $\rm \overline N=−1$
$\rm M=−Fl$ ; $\rm \overline M=−l$

Partie BC :

$\rm N=0$ ; $\rm \overline N=0$
$\rm M=F (\mathcal x−l)$ ; $\rm \overline M= (\mathcal x−l)$

$\rm \displaystyle\lambda_{vertical}=\int_0^h \left[\frac{Fl^2}{EI} + \frac{F}{ES}\right]\mathcal{dy}$ $+$ $\rm \displaystyle\int_0^l \left[\frac{F(\mathcal x−l )^2}{EI} +0\right]\cal dx$
$\rm \displaystyle\lambda_{vertical}=\left[\dfrac{Fl^2h}{EI} + \dfrac{Fh}{ES}\right] + \dfrac{Fl^3}{3EI}$ $\rm = \dfrac{F}{E} \left[\dfrac{l^2}{3 I} (3 h+l) + \dfrac{h}{S}\right]$

Déplacement horizontal (système auxiliaire n° 2) selon la force unité.

Partie AB :

$\rm N=−F$ ; $\rm \overline N=0$
$\rm M=−Fl$ ; $\rm \overline M=−h+ \cal y$

Partie BC :

$\rm N=0$ ; $\rm \overline N=1$
$\rm M=F (\mathcal x−l)$ ; $\rm \overline M=−h+h=0$

$\rm \displaystyle \lambda_{Horizontal} = \int_0^h \left[\dfrac{Fl}{EI} (h−\mathcal y)+0\right]\mathcal{dy}$ $+$ $\rm \displaystyle \int_0^l [0 ]\mathcal{dx}$ $\rm \displaystyle=−\int_0^h \left[\dfrac{Fl}{EI} (\mathcal y−h)\right]\mathcal{dy}$ $\rm =\dfrac{Flh^2}{2 EI}$

Remarque : Cette méthode permet d’avoir des calculs plus courts (pas de dérivées partielles) et donc avec moins de risques d’erreurs, mais il faut faire les systèmes auxiliaires avec les bonnes hypothèses.

Objectif : calculer le déplacement au milieu de la poutre.

Si on utilise le théorème de Castigliano et les équations associées, il faut rajouter une Force $\rm F =0$.

$\rm PFS : \Rightarrow Y_A=\dfrac{(\mathcal{ql}+F)}{2} =Y_B$ ; $\rm X_A=0$

La symétrie de charge et la symétrie géométrique nous permettront de n’étudier la poutre que sur le premier intervalle, puis on multipliera les effets par $2$.

$0\leq x \leq \dfrac{l}{2}$ $\Rightarrow \mathrm M(x)=\dfrac{−qx^2}{2} + \dfrac{(ql+\rm F)}{2} x$ $\Rightarrow \dfrac{\partial \mathrm M(x)}{\partial \rm F} = \dfrac{x}{2}$
$\displaystyle \mathrm{EI} \lambda =2\int_0^{\frac{l}{2}} \left[\dfrac{−qx^2}{2} + \dfrac{(ql+\mathrm F)}{2}x\right]\dfrac{x}{2} dx$ $\displaystyle =\int_0^{\frac{l}{2}} \left[\dfrac{−qx^3}{2} + \dfrac{(ql+\mathrm F)}{2} x^2\right]dx$ $=\left[\dfrac{−qx^4}{8} + \dfrac{(ql+\mathrm F)}{6} x^3\right]_0^{\frac{l}{2}}$ $=\left[\dfrac{−q \left(\frac{l}{2}\right)^4}{8} + \dfrac{(ql+\mathrm F)}{6} \left(\dfrac{l}{2}\right)^3\right]_0^{\frac{l}{2}}$
$\mathrm{EI} \lambda = \dfrac{−ql^4}{128} + (ql +\mathrm F)\dfrac{l^3}{48}$ ; $\rm F=0$ $\Rightarrow \mathrm{EI} \lambda = \dfrac{−ql^4}{128} + \dfrac{ql^7}{48}$ $= \dfrac{−3 ql^4}{384} + \dfrac{8 ql^4}{384}$ $= \dfrac{5 ql^4}{384}$ $\Rightarrow \lambda = \dfrac{5 ql^4}{384\rm EI}$

Même objectif avec la méthode de Fontviolant.

$\rm PFS$ (système principal) : $\rm X_A=0$ ; $\rm Y_A=Y_B=\dfrac{\mathcal{ql}}{2}$

$\rm PFS$ (système auxiliaire) : $\rm X_A=0$ ; $\rm Y_A=Y_B=\dfrac{1}{2}$

$0\leq x \leq \dfrac{l}{2} \Rightarrow \mathrm M_{(x)} =\dfrac{−qx^2}{2} + qlx$ ; $\overline{\mathrm M_{(x)}} = \dfrac{x}{2}$

$\mathrm{EI} \displaystyle \lambda =2\int_0^{\frac{l}{2}} \left[\dfrac{−qx^2}{2} + qlx\right]\dfrac{x}{2} dx$ $\displaystyle =\int_0^{\dfrac{l}{2}} \left[\dfrac{−qx^3}{2} + qlx^2\right]dx$ $=\left[\dfrac{−q\left(\frac{l}{2}\right)^4}{8} + \dfrac{ql\left(\frac{l}{2}\right)^3}{6}\right]_0^{\frac{l}{2}} =\dfrac{5ql^4}{384}$ $\Rightarrow \lambda = \dfrac{5 ql^4}{\rm 384 EI}$

Chargement uniformément réparti. Résolution par la méthode de Fontviolant.

L’objectif est de calculer l’action mécanique en $\rm B$ pour ce système hyperstatique d’ordre $1$.

En $\rm B$ il n’y a pas de déplacement, donc : $\lambda =0$

$\rm PFS : \begin{array}{lll}\rm X_A=0 ~; \rm Y_A+Y_B−\mathcal{ql} = 0\\
\mathrm{M_A+Y_B} l-\dfrac{ql^2}{2} =0\\
\mathrm{MA}= \dfrac{ql^2}{2}−\mathrm{Y_B} l\\
\rm Y_A=\mathcal{ql}−Y_B\end{array}$

Les inconnues de liaisons sont toutes définies en fonction de $\rm Y_B$ qui sera considérée comme inconnue principale.

$\mathrm M_{(x)}=\displaystyle −\sum \mathrm{MF_G}$ $= \dfrac{−qx^2}{2} + (ql−\mathrm{Y_B}) x−\left(\dfrac{ql^2}{2} −\mathrm{Y_B}l\right)$
$\mathrm M_{(x)} = \dfrac{−qx^2}{2} + qlx−\mathrm{Y_B} (x−l)− \dfrac{ql^2}{2}$
$\overline{\mathrm M_{(x)}} = l−x = −( x−l)$ $\mathrm{EI} \lambda =0=$ $\displaystyle −\int_0^l \left[\dfrac{−qx^2}{2} + qlx \mathrm{Y_B} (x−l )−\dfrac{ql^2}{2}\right]$ $( x−l) dx$
$\mathrm{EI} \lambda =0 \displaystyle =−\int_0^l \left[\frac{−qx^3−qlx^2}{2} + qlx^2−ql^2x\right.$ $−$ $\left.\mathrm{Y_B} (x−l)^2−\frac{ql^2}{2} (x−l )\right]dx$
$\mathrm{EI} \lambda =0=−\left[\dfrac{−qx^4}{8} − \dfrac{qlx^3}{6} −\dfrac{qlx^3}{3} − \dfrac{ql^2x^2}{2} − \mathrm{Y_B} \dfrac{(x−l)^3}{3} − \dfrac{ql^2}{4} (x−l)^2\right]_0^l$
$\mathrm{EI} \lambda=0=\left[−\dfrac{ql^4}{8} − \dfrac{ql^4}{6} − \dfrac{ql^4}{3} − \dfrac{ql^4}{2}\right.$ $−$ $\left.\mathrm{Y_B} \dfrac{(l−l )^3}{3} −\dfrac{ql^2}{4} (l−l)^2−\left(−\mathrm{Y_B} \dfrac{l^3}{3} − \dfrac{ql^4}{4}\right)\right]$
$\mathrm{EI} \lambda=0=\left[\dfrac{−9 ql^4}{8} + \dfrac{ql^4}{4} \mathrm{Y_B}\dfrac{l^3}{3}\right]$ $=\left[\dfrac{−ql^4}{8} + \mathrm{Y_B} \dfrac{l^3}{3}\right]$
$\Rightarrow \mathrm{Y_B} =\dfrac{3 ql}{8}$ $\Rightarrow \mathrm{Y_A}=\dfrac{5 ql}{8}$ $\Rightarrow  \mathrm{MA} =\dfrac{ql^2}{8}$