Poutres hyperstatiques
Poutre hyperstatique d’ordre $1$ à deux travées identiques. Résolution par la méthode d’intégration du moment fléchissant.
$\text{Inconnues de liaison}$
$\rm X_A$, $\rm Y_A$, $\rm Y_B$, $\rm Y_C$ $\rm\Rightarrow I=4$
$d=\rm I−E = 4−3 = 1 \Rightarrow ordre~1$
L’équation de la déformée se calcule sur chaque travée, ce qui donne $4$ constantes d’intégration ($2$ par travée). Il faut ajouter l’inconnue hyperstatique, ce qui oblige à trouver au moins $5$ conditions aux limites.
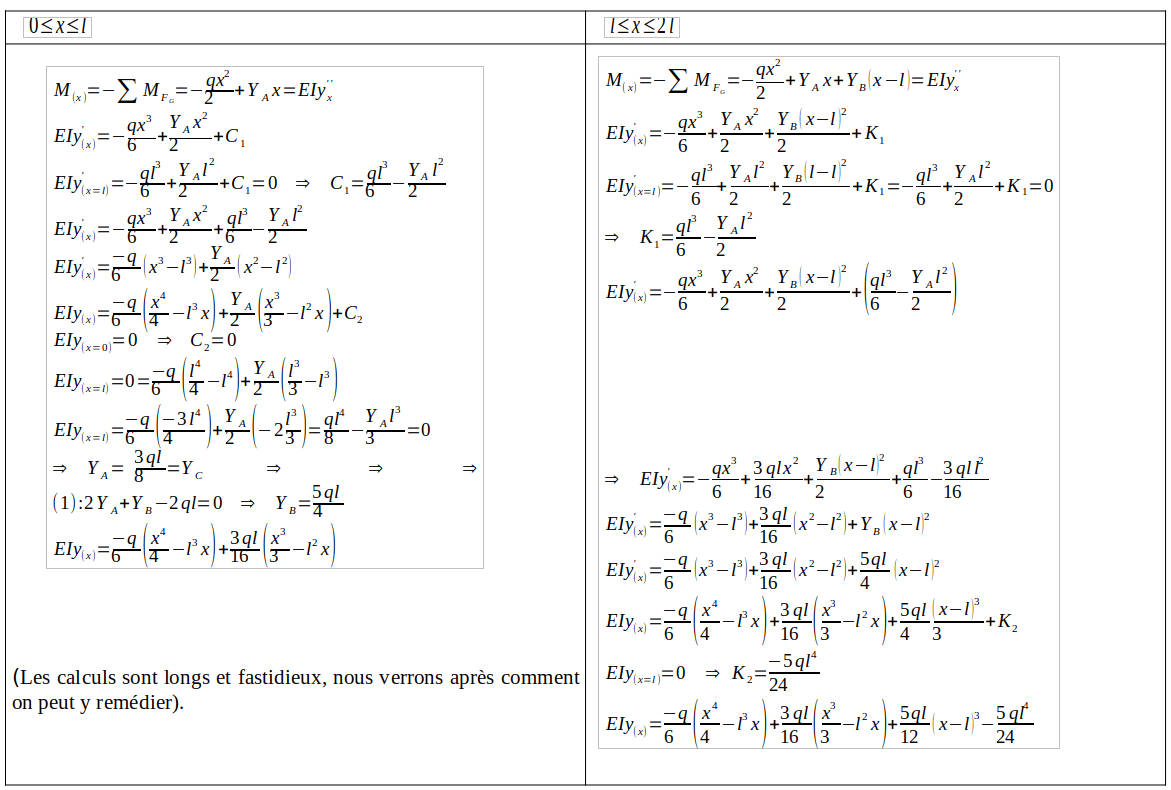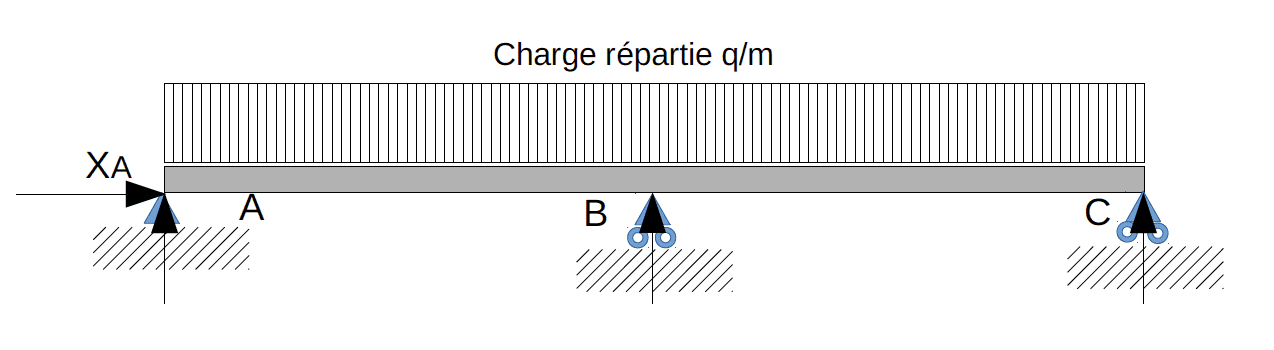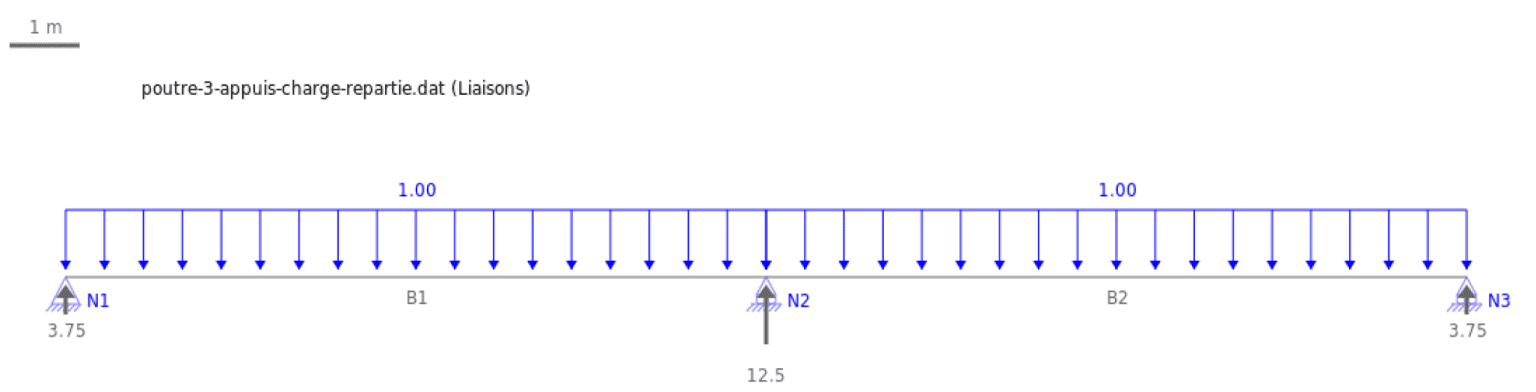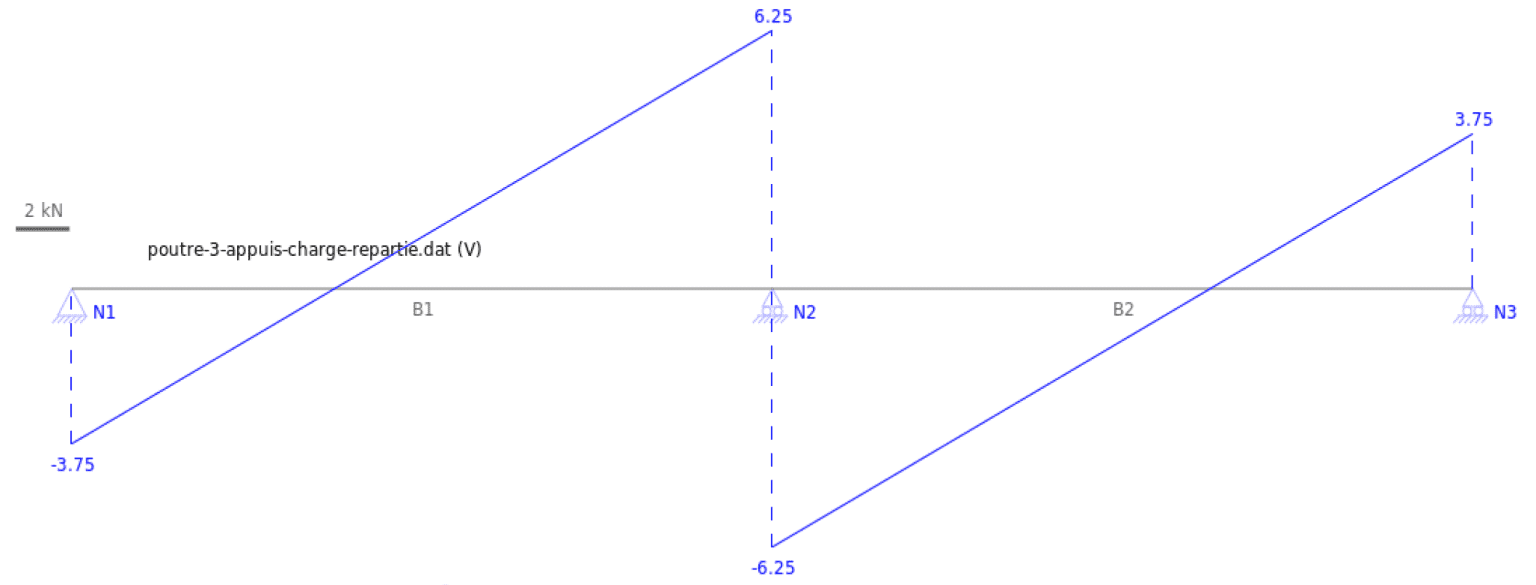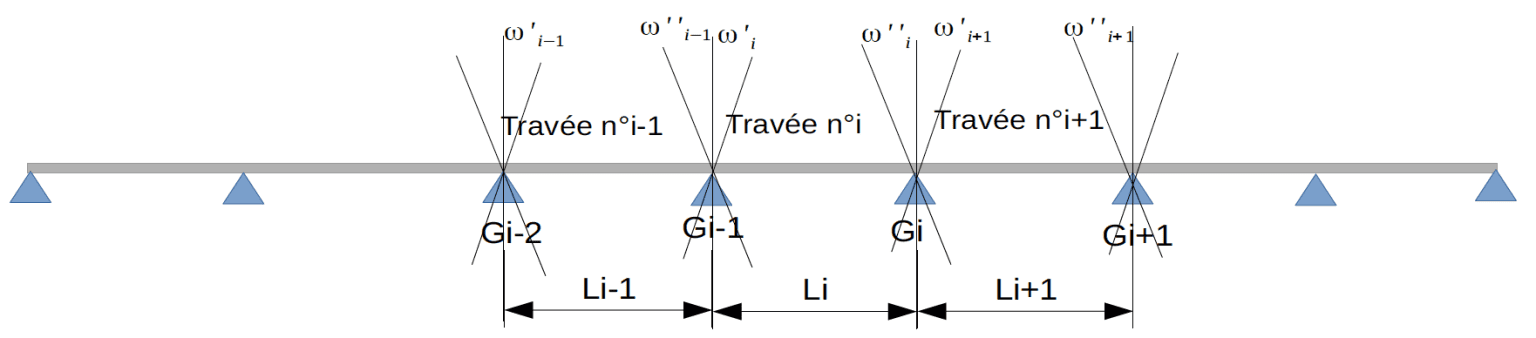
Pour la travée $\rm n° i$, nous aurons :
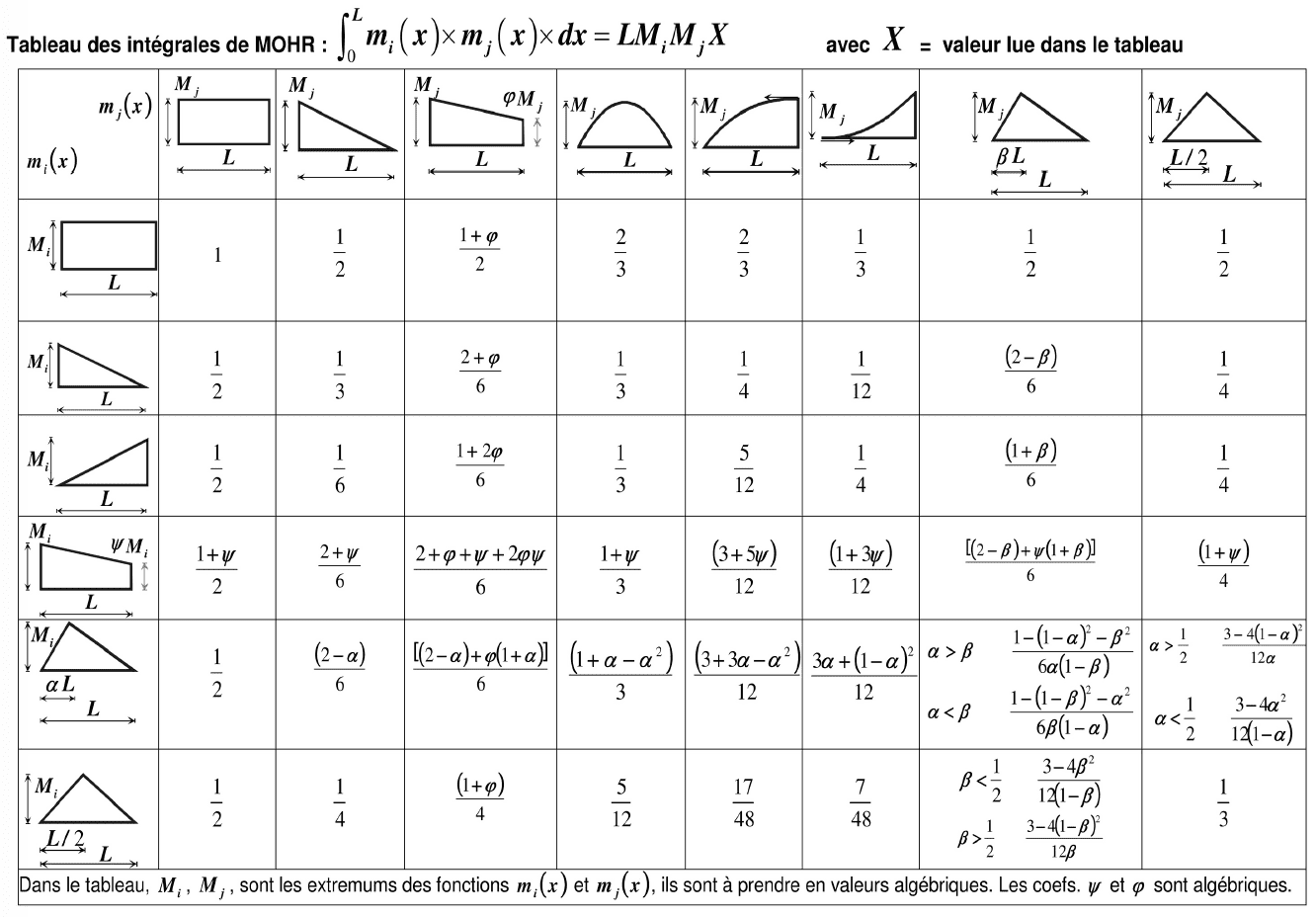
$\displaystyle a=\int^{\rm L_i}_{0}\left(1 - \dfrac{x}{\rm L_i}\right)^2\dfrac{dx}{\mathrm{EI}_{(i,x)}}$ ; $\displaystyle b=\int^{\rm L_i}_{0}\dfrac{x}{\rm L_i}\times \left(1-\dfrac{x}{\rm L_i}\right)\dfrac{x}{\mathrm{EI}_{(i,x)}}$ ; $\displaystyle c=\int^{\rm L_i}_0\left(\dfrac{x}{\rm L_i}\right)^2\dfrac{dx}{\mathrm{EI}_{(i,x)}}$
Si $\rm I_i(x) = constante = I_i$ $\Rightarrow a = 2b = c = \dfrac{\rm L_i}{3 \rm EI_i}$
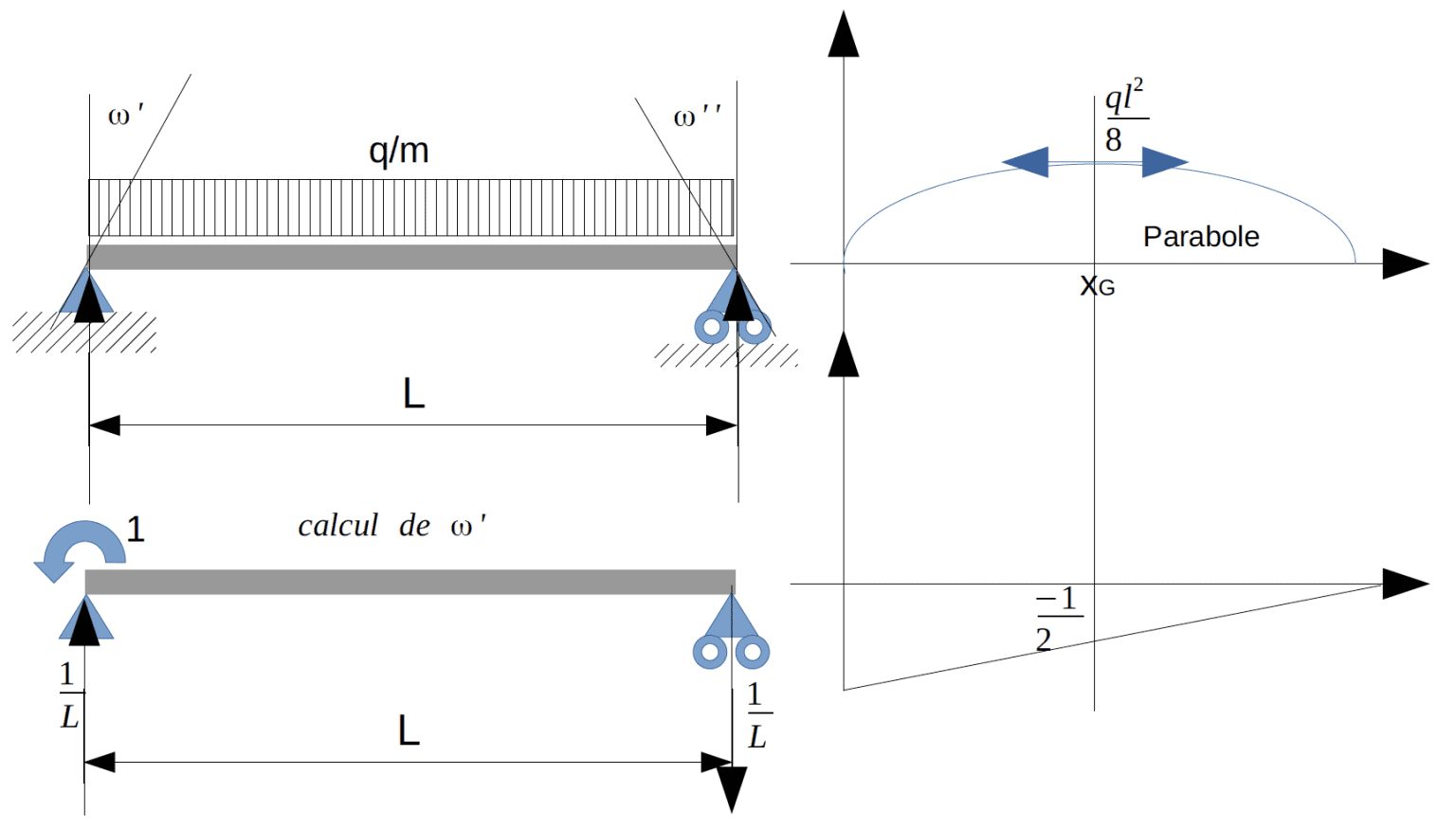
$\displaystyle \omega'_i=−\int^{\rm L_i}_0\left(1 - \dfrac{x}{\rm L_i}\right) \dfrac{\mu_{(x)}}{\mathrm{EI}_{(i,x)}}dx$ ; $\displaystyle\omega''_i=\int^{\rm L_i}_0\left(\dfrac{x}{\rm L_i}\right)\dfrac{\mu_{(x)}}{\mathrm{EI}_{(i, x)}}dx$ les rotations aux appuis.
$\mu$ les moments fléchissants de chaque travée isostatique si déplacements $d_i$ et $d_{i−1}$ des appuis :
$\Omega_i=
\dfrac{d_i−d_{i−1}}{\rm L_i}$
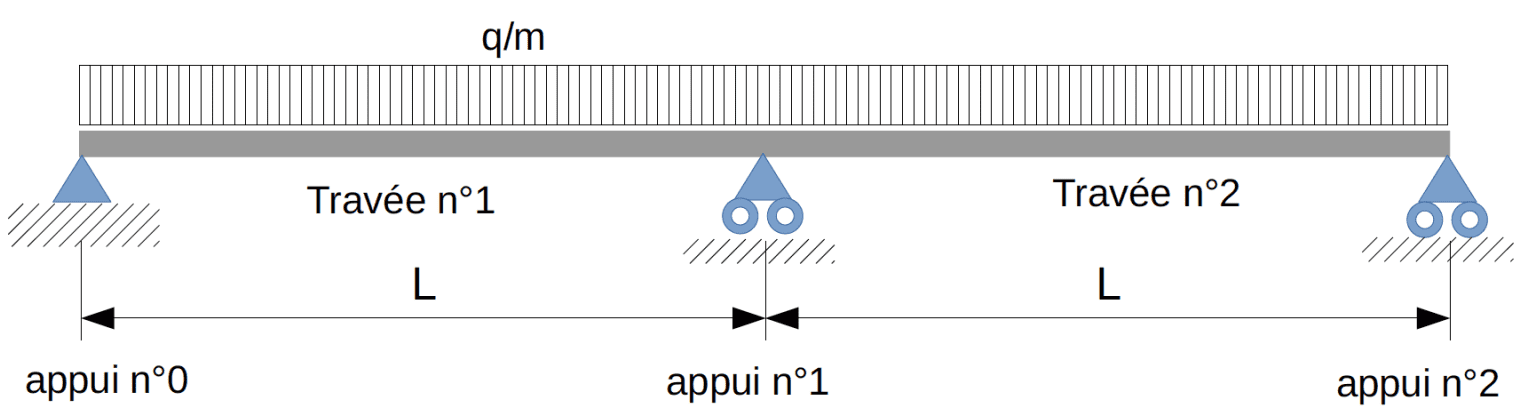
Formule des trois moments pour l’appui $\mathrm n°i$ :
$b_i \mathrm{M_{i−1}} + (a_{i+1} + c_i)\mathrm{M_i} + b_{i+1}\mathrm{M_{i +1}}$ $\rm =\omega'_{i + 1}−\omega''_i + \Omega_{i+1}−\Omega_i$
La plupart du temps, il n’y a pas de déplacement au niveau des appuis, donc les $\Omega$ sont nuls.
$\Rightarrow b_i \mathrm{M_{i−1}} +(a_i+1+c_i)\mathrm{M_i}+b_{i+1}\mathrm{M_{i+1}}$ $=\omega'_{ i+1}−\omega''_i$
Lorsque $\rm E$ et $\rm I$ sont constants, alors la formule des trois moments devient :
$\rm M_{i−1} \rm L_i+ 2 (L_i+L_{i+1})M_i+L_{i+1}M_{i+1}$ $=6\rm EI (\omega'_{i+1}−\omega''_i)$
C’est cette expression qui sera la plus couramment employée.
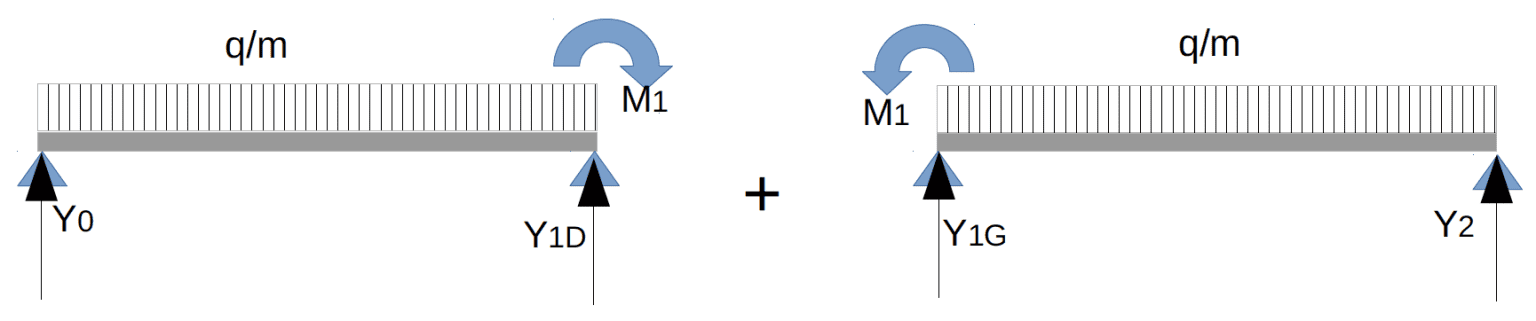
Efforts internes à partir de la formule des trois moments. Pour la travée $\rm n°i$ et de longueur $\rm L_i$ :
$\rm M_i−1 L_i+2 (L_i+L_{i+1})M_i+L_{i+1}M_{i+1}$ $=6\mathrm{EI}(\omega'_{i+1}−\omega''_i)$
$\rm V_{i(\mathcal x)}=V_{iso(\mathcal x)} +\left(\dfrac{M_{i−1}−M_i}{L_i}\right)$ ; $\rm M_{i(\mathcal x)} = M_{iso(\mathcal x)} + M_{i−1} \left(1−\dfrac{\mathcal x}{L_i}\right)+M_i\dfrac{\mathcal x}{L_i}$
avec :
Soit $\lambda =$ déplacement du point étudié, $\rm M =$ moment fléchissant, $\rm \overline M =$ moment fléchissant du système unitaire associé.
$\displaystyle \rm\lambda=\int\dfrac{M \overline M}{EI} \cal dx$ avec $\rm M$ de la forme $\displaystyle ax+b \Rightarrow \lambda =\int(ax +b)\dfrac{\rm M}{\rm EI}dx$ $\displaystyle =a\int \dfrac{x\rm M}{\rm EI} dx+b \int \dfrac{\rm M}{\rm EI} dx$
Le premier terme correspond au moment statique de l’aire $\displaystyle\int\dfrac{\rm M}{\rm EI}dx$ dont le bras de levier du $\rm CDG$ sera $\rm \overline X$.
Le deuxième terme correspond à l’aire $\rm (A)$ sous la courbe de $\mathrm M_{(x)}$. On peut écrire :
$\lambda =a\mathrm{\overline X A}+b \mathrm A = A(a \overline{\mathrm X} + b) = \rm A\overline{M_{(\overline X)}}$
Ce qui donne :
$\lambda =$ (Aire de la surface du moment fléchissant) $\times$ (Valeur du moment fléchissant virtuel au $\rm CDG$ du moment réel)
Exemple : Poutre encastrée avec une charge ponctuelle à l’extrémité.
Calcul du déplacement de l’extrémité avec le système auxiliaire n° 1 :
$\rm A = \dfrac{−Pl^2}{2}$ et $\rm \overline{M_{\text{CDG de A})}} = \dfrac{−2l}{3}$ $\rm \Rightarrow EI \lambda = \left(\dfrac{−Pl^2}{2}\right) \times \left(\dfrac{−2l}{3}\right) = \dfrac{Pl^3}{3}$
$\rm \lambda= \dfrac{Pl^3}{3 EI}$
Calcul de la rotation d’extrémité avec le système auxiliaire n° 2 :
$\rm A = \dfrac{−Pl^2}{2}$ et $\rm\overline{M_{(\text{CDG de A})}} = -1$ $\rm \Rightarrow EI \varphi = \left(\dfrac{−Pl^2}{2}\right) \times (-1) = \dfrac{Pl^2}{2}$
$\rm\varphi = \dfrac{Pl^2}{2 EI}$
Pour un moment fléchissant en parabole en chapeau, l’aire sera :
$\rm A=\dfrac{2}{3} \times L \times \dfrac{Pl^2}{8}$
Pour les surfaces plus complexes, il vaut mieux utiliser le tableau des intégrales de Mohr.
Reprenons l’exercice précédent :
Le calcul de la rotation sur l’appui de gauche sera mené avec la méthode des aires et la schématisation de Fontviolant.
$\mathrm{Aire}=\dfrac{2 \rm L}{3} \times \dfrac{q\rm L^2}{8} =\dfrac{q\rm L^3}{12}$ $\Rightarrow \omega'=\dfrac{q\rm L^3}{12\rm EI} \times\left(\dfrac{−1}{2}\right) = \dfrac{−q\rm L^3}{24 \rm EI}$ $\Rightarrow \omega'' = \dfrac{q\rm L^3}{24\rm EI}$
(valeur qu’il est bon de retenir car très fréquemment utilisée)
Formule des trois moments pour la travée n° 1 :
$\rm M_{i−1}L_i+2(L_i + L_{i+1}) M_i + L_{i+1} M_{i + 1}$ $\rm = 6 EI (\omega'_{i +1} − \omega''_i)$ devient : $\rm M_0 L_1+2 (L_1+L_2 )M_1 + L_2 M_2$ $\rm = 6 EI (\omega'_2 − \omega''_1)$ avec : $\rm M_0=M_2=0$ $\text{(articulation et appui simple)} \rm\Rightarrow \dfrac{2L}{3 EI} M_1$ $\rm = \dfrac{−\mathcal qL^3}{24 EI} − \dfrac{\mathcal qL^3}{24 EI} = \dfrac{−\mathcal qL^3}{12 EI}$ $\rm\Rightarrow M_1= \dfrac{−\mathcal qL^2}{8}$
Pour trouver les réactions d’appuis, il suffit de faire le PFS sur une travée isostatique en y incluant $\rm M_1$.
L’action $\rm Y_1$ se déduira de la somme (par superposition des systèmes) en faisant :
$\rm Y_{1G} + Y_{1 D} = Y_1$
Après calculs et en utilisant les symétries, on trouve :
$\rm Y_0 = \dfrac{3\mathcal qL}{8}$ ;
$\rm Y_1=Y_{1G} + Y_{1 D} = \dfrac{5\mathcal qL}{4}$ ;
$\rm Y_2=\dfrac{3\mathcal qL}{8}$
