Statistiques descriptives

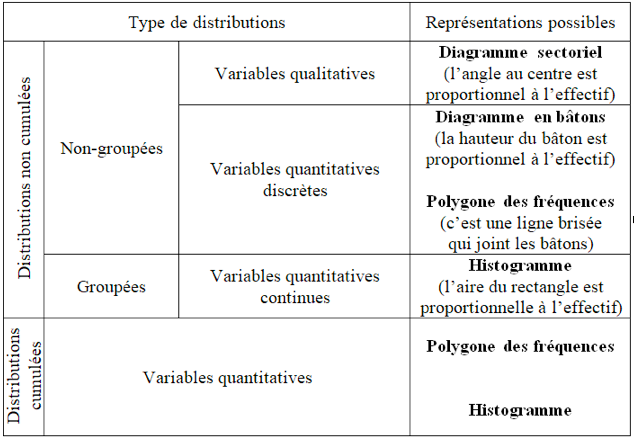
Paramètres de position des variables quantitatives

• Moyenne :
  

Série de $p$ valeurs: $m=\displaystyle\frac{x_1+x_2+...+x_p}{p}$

Si la variable est quantitative continue discrétisée on utilise la formule en remplaçant $x_i$ par le milieu de la classe. On obtient alors en réalité une approximation de la moyenne.  

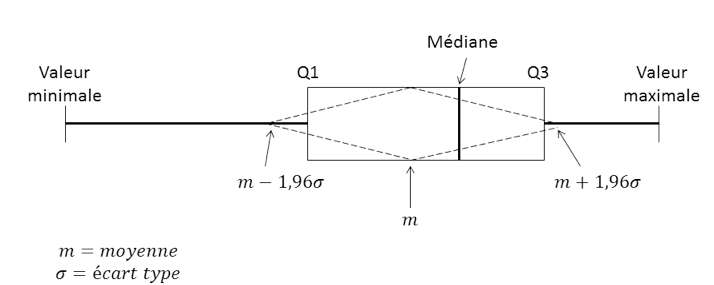
• Médiane : elle partage la série de données en deux groupes de même effectif 
• Mode : c'est la valeur qui a la fréquence la plus grandeRemarque : 

Pour des distributions symétriques (par exemple la loi normale), il y a égalité entre mode, médiane et moyenne.

• Quartiles : ils partagent la série de données en quatre groupes de même effectif : Q1, Q2 (médiane), Q3

• $q\mathrm{^{ème}}$ quantile : valeur en dessous de laquelle se trouvent $q\%$ des observations. Par exemple le $\mathrm{25^{ème}}$ quantile correspond à $Q1$.

Paramètres de dispersion des variables quantitatives

• Variance $s^2$ :

Série de $p$ valeurs :

$s^2=\displaystyle\frac{1}{p}\sum_{i=1}^p(x_i m)^2=\displaystyle\frac{1}{p}(\sum_{i=1}^px_i^2)-m^2$    

• Ecart type : racine carrée de la variance 

• Extrêmes : valeurs minimale et maximale.

• Etendue : valeur maximale-valeur minimale.

• Coefficient de variation : $CV=\frac{s}{m}$ (exprimé en pourcentage).

Représentations graphiques

Diagramme de Tuckey

Le diagramme de Tuckey est aussi appelé box-plot ou boîte à moustaches. Il permet de représenter des paramètres de la variable étudiée.