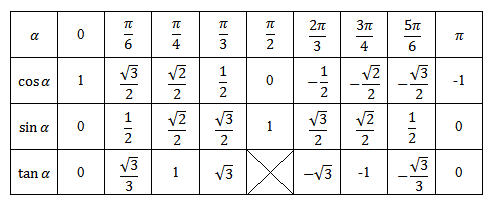
Fonctions cosinus et sinus
Les fonctions cosinus et sinus sont définies, continues et dérivables sur R.
Elles sont périodiques de période 2π et leur représentation graphique est une sinusoïde de période 2π.
Pour tout x∈R, cos′(x)=−sin(x) et sin′(x)=cos(x).
Pour tout (a,b)∈R2 :
- cos(a+b)=cos(a)cos(b)−sin(a)sin(b)
- sin(a+b)=sin(a)cos(b)+sin(b)cos(a)
La fonction cosinus est paire donc elle est symétrique par rapport à l'axe des ordonnées.
La fonction sinus est impaire donc elle est symétrique par rapport à l'origine du repère.
Fonction tangente
La fonction tangente est définie, continue et dérivable sur les intervalles ]−π2+kπ;π2+kπ[ avec k réel.
Elle est périodique de période π.
Pour tout x∈]−π2+kπ;π2+kπ[ avec k réel, tan′(x)=1+tan2(x)=1cos2(x).
La fonction tangente est impaire donc elle est symétrique par rapport à l'origine du repère.