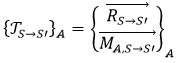Mécanique - Principe fondamental de la statique

Base orthonormée directe :

Une base orthonormée est une base constituée de vecteurs de norme égale à $1$ et orthogonaux $2$ à $2$. Par exemple en $\rm 3D$ la base $\rm (\overrightarrow{e_{1}},\overrightarrow{e_{2}},\overrightarrow{e_{3}})$ est orthonormée si et seulement si $\forall (i,j) \in [[ 1,3 ]]^{2}$,  $\overrightarrow{e_{i}}.\overrightarrow{e_{j}}=\delta_{ij}$ avec $\delta_{ij}=1$ si $i=j$, $0$ sinon.

Une base orthonormée $\rm (\overrightarrow{e_{1}},\overrightarrow{e_{2}},\overrightarrow{e_{3}})$ est directe si et seulement si la matrice dont les colonnes sont les vecteurs de la base a un déterminant égal à $+1$. Autrement dit avec le principe des $3$ doigts on doit respecter l’ordre suivant :

• Le pouce $\rm \rightarrow \overrightarrow{e_{1}}$
• L’index $\rm \rightarrow \overrightarrow{e_{2}}$
• Le majeur $\rm \rightarrow \overrightarrow{e_{3}}$

Une base orthonormée directe couramment utilisée en mécanique est la base canonique $(\overrightarrow{x},\overrightarrow{y},\overrightarrow{z})$ avec $\overrightarrow{x}=(1,0,0)$ ; $\overrightarrow{y}=(0,1,0)$ ; $\overrightarrow{z}=(0,0,1)$.

Opérations sur les vecteurs :

Soient $3$ vecteurs $(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w})$ de $\mathbb{R}^{3}$, soit $\lambda \in \mathbb{R}$.

Produit scalaire :

• $\overrightarrow{u}\cdot \overrightarrow{v}=\overrightarrow{v}\cdot \overrightarrow{u}$
• $\overrightarrow{u}\cdot (\overrightarrow{v} + \lambda\overrightarrow{w})$ $= \overrightarrow{u}\cdot \overrightarrow{v}+\lambda\overrightarrow{u}\cdot \overrightarrow{w}$
• $\overrightarrow{u}\cdot \overrightarrow{v} = \overrightarrow{0}$ si et seulement si $\overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux.
• Si $\overrightarrow{u} = (x,y,z)$ et $\overrightarrow{v} = (x’,y’,z’)$ alors $\overrightarrow{u} \cdot \overrightarrow{v} = xx’ + yy’ + zz’$

Produit vectoriel :

• $\overrightarrow{u} \wedge \overrightarrow{v} = - \overrightarrow{v} \wedge \overrightarrow{u}$
• $\overrightarrow{u} \wedge (\overrightarrow{v} + \lambda\overrightarrow{w})$ $= \overrightarrow{u} \wedge \overrightarrow{v} + \lambda\overrightarrow{u} \wedge \overrightarrow{w}$
• $\overrightarrow{u} \wedge \overrightarrow{v} = \overrightarrow{0}$ si et seulement si $\overrightarrow{u}$ et $\overrightarrow{v}$ sont colinéaires.

Projections :

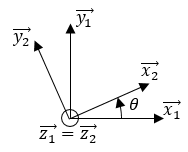
Soit la figure suivante :

Projeter un vecteur suivant un axe revient à faire le produit scalaire entre ce vecteur et le vecteur directeur de l’axe. Par exemple :

• Projeter le vecteur $\overrightarrow{x_{2}}$ suivant l’axe dirigé par $\overrightarrow{x_{1}}$ revient à calculer $\overrightarrow{x_{2}}\cdot \overrightarrow{x_{1}} = \cos(\theta)$
• Projeter le vecteur $\overrightarrow{y_{1}}$ suivant l’axe dirigé par $\overrightarrow{x_{2}}$ revient à calculer $\overrightarrow{y_{1}}\cdot \overrightarrow{x_{2}} = \sin(\theta)$.

Torseurs :

Un torseur est une manière d’écrire un champ de vecteurs et peut être décrit par $3$ paramètres : $2$ vecteurs et un point d’application.

En statique le torseur des actions mécaniques en un point $\mathrm A$ d’un solide $\mathrm S$ exercées sur un solide $\mathrm S’$ s’écrit :

Le torseur respecte la formule de Varignon, en connaissant $\rm \overrightarrow{M_{A,S \rightarrow S’}}$ et le vecteur $\rm \overrightarrow{BA}$, on peut connaître $\rm \overrightarrow{M_{B,S \rightarrow S’}}$ : $\rm \overrightarrow{M_{B,S \rightarrow S’}}$ $\rm =\overrightarrow{M_{A,S \rightarrow S’}}+\overrightarrow{BA} \wedge \overrightarrow{R_{S \rightarrow S’}}$.

La résultante $\rm \overrightarrow{R_{S \rightarrow S’}}$ est inchangée par changement de point.

Degrés de liberté :

Les degrés de liberté d’un solide $\mathrm S$ par rapport à un solide $\mathrm S’$ sont les possibilités de mouvements autorisés entre ces $2$ solides. En $3$ dimensions, dans un repère $\mathrm R=(O, \overrightarrow{x},\overrightarrow{y},\overrightarrow{z})$ orthonormé direct, il y a au maximum $3$ rotations (et donc $3$ composantes de vitesse de rotation) autour des $3$ axes $\overrightarrow{x},\overrightarrow{y}$ et $\overrightarrow{z}$ ainsi que $3$ translations (et donc $3$ composantes en vitesse de translation) au maximum suivant ces mêmes axes.

Notion d’action mécanique :

Par définition une action mécanique est un phénomène physique susceptible de mettre en mouvement ou de déformer un solide. Les actions mécaniques peuvent être décomposées en $2$ familles : Les forces en tout point du solide considérés et les moments appliqués en un point du solide considéré. La force est l’action mécanique qui a tendance à provoquer la translation d’un solide suivant l’axe de la force. Le moment est l’action mécanique qui a tendance à faire tourner un solide autour d’un axe. Le moment peut être engendré par un effort, par exemple appuyer sur une poignée de porte la fait pivoter autour de son axe.

Torseur associé à une liaison parfaite :

Pour toutes les liaisons sauf l’hélicoïdale, si un mouvement de rotation est autorisé suivant un axe, alors le moment autour de ce même axe au point d’application de la liaison est nul.

Pour toutes les liaisons sauf l’hélicoïdale, si un mouvement de translation est autorisé suivant un axe, alors la résultante suivant ce même axe est nul.

Pour la liaison hélicoïdale modélisée au point $\mathrm A$, la vitesse de rotation $\overrightarrow{\omega}$ et la vitesse de translation $\overrightarrow{V_{A}}$ dans l’axe de la liaison sont liées par le pas de liaison $p$ : $\displaystyle \overrightarrow{\rm V_{A}}=\pm \frac{p}{2\pi}\overrightarrow{\omega}$, le signe dépendant de l’orientation du pas ($+$ si à droite ou $–$ si à gauche). Le même type de relation lie le moment $\rm \overrightarrow{M_{A}}$ autour de l’axe de la liaison à l’effort $\rm \overrightarrow{F}$ suivant ce même axe : $\displaystyle\overrightarrow{\rm M_{A}}=\pm \frac{p}{2\pi}\overrightarrow{\mathrm F}$.

Frottement :

Si $2$ solides sont en contact frottant, alors la résultante des efforts en un point de contact peut se décomposer en une composante tangentielle à la normale de contact $\rm \overrightarrow{T}$ et une composante parallèle à la normale de contact $\rm \overrightarrow{N}$. Les normes de ces $2$ vecteurs sont liées par la loi de Coulomb :

$||\overrightarrow{\mathrm T}|| \leq f||\overrightarrow{ \mathrm N}||$ où $f$ est le coefficient de frottement entre les $2$ solides. Lorsqu’il y a glissement entre les $2$ solides on a égalité.

Un système de solides indéformables peut être modélisé par un schéma cinématique, dans lequel à chaque liaison est associé un torseur des actions mécaniques. On peut associer à ce schéma cinématique un graphe des liaisons répertoriant les numéros des solides, le nom/axe/point d’application de chaque liaison entre $2$ solides ainsi que les actions mécaniques extérieures qui s’exercent sur le système.

Pour appliquer le Principe Fondamental de la Statique $\rm (PFS)$ :

1. Isoler un solide ou ensemble de solides.
2. Faire le bilan des actions mécaniques extérieures appliquées à l’isolement, les traduire sous forme de torseurs (ne pas oublier le point d’application de chaque torseur).
3. Appliquer la formule de Varignon et ramener tous les torseurs au point correspondant à la liaison avec le plus d’inconnues.
4. Par le $\rm PFS$ la somme des vecteurs forces est nulle et la somme des vecteurs moments au point choisi est nulle.

En $3$ dimensions il y a $3$ composantes d’efforts et $3$ composantes en moment ce qui donne un système de 6 équations. En $2$ dimensions il y a $2$ composantes d’effort dans le plan considéré et une composante en moment suivant l’axe normal au plan, soit $3$ équations.

Notion d’isostatisme et d’hyperstatisme :

Lors du choix de l’isolement d’un ensemble de solides, il faut faire attention au nombre d’inconnues statiques qui entreront en jeu dans le système d’équations issu du $\rm PFS$. En $3$ dimensions il y a 6 équations, pour que le système soit solvable (c’est-à-dire que les inconnues statiques sont déterminables) il faut au maximum $6$ inconnues statiques. En $2$ dimensions il y a $3$ équations, il faut alors au maximum $3$ inconnues statiques pour que le système soit solvable. Si il y a autant d’équations que d’inconnues on dit que le système et isostatique. Lorsqu’il y a plus d’inconnues que d’équations, on dit que le système est hyperstatique. Le degré d’hyperstatisme $h$ s’exprime en fonction du nombre d’équations indépendantes $\rm N_{eq}$ et du nombre d’inconnues statiques $\rm I_{s}$ : $h= \rm I_{s} - N_{eq}$. $h$ est toujours positif ou nul.