Fonctions

Fonction exponentielle

La fonction exponentielle est la fonction $x \mapsto e^{x}$. Elle est définie, continue, dérivable, strictement croissante et strictement positive sur l'ensemble des nombres réels. La fonction exponentielle est sa propre dérivée.

Propriétés :

$e^0 = 1$

Pour tous nombres réels $a$ et $b$ : $e^{a + b} = e^{a} \times e^{b}$ ; $e^{-a} = \frac{1}{e^{a}}$ ; $e^{a - b} = \frac{e^{a}}{e^{b}}$ ; ${(e^{a})}^{n} = e^{n a}$ ($n$ entier naturel).

Pour une fonction $u$ dérivable sur un intervalle $I$, $e^{u}$ est dérivable sur $I$ et $(e^{u})' = u’ \times e^{u}$ sur cet intervalle.

Fonction logarithme népérien

La fonction logarithme népérien définie sur $]0 ; + \infty[$ est la fonction $x \mapsto \ln(x)$ où le nombre réel $\ln(x)$ est l’unique solution de l’équation $e^{y} = x$ d’inconnue $y$.

Elle est définie, continue, dérivable sur l’intervalle $]0 ; + \infty[$.

Pour tout $x \in\:]0 ; + \infty[$, $\ln’(x) = \frac{1}{x} > 0$ donc la fonction $\ln$ est strictement croissante sur l’intervalle $]0 ; +\infty[$.

$\ln(1) = 0$ et $\ln x < 0$ pour $x \in \:]0 ; 1[$ et $\ln x >$ 0 pour $x \in \:]1 ; + \infty[$ car la fonction $\ln$ est strictement croissante sur l’intervalle $]0 ; + \infty[$.

Propriétés :

Pour tous les réels $a$ et $b$ strictement positifs :

$\ln(a \times b) = \ln(a) + \ln(b)$ ; $\ln(\frac{1}{b}) = -\ln(b)$ ;  $\ln(\frac{a}{b}) = \ln(a) - \ln(b)$ ; $\ln({a}^{n}) = n \ln(a)$ ($n$ entier naturel) ; $\frac{1}{2} \ln(a) = \ln(\sqrt{a})$.

Pour une fonction $u$ strictement positive et dérivable sur un intervalle $I$, $\ln(u)$ est dérivable sur $I$ et $(\ln(u))’ = \frac{u'}{u}$ sur cet intervalle.

Dérivée d'un produit par un réel

Si $u$ est une fonction dérivable sur un intervalle $I$ de $\mathbb{R}$ et si $k$ est un réel, alors la fonction $k \times u$ est dérivable sur  $I$ et on a :

$(k \times u)' = k \times u'$.

Exemple : 

$u(x) = 3{x}^2 ; u'(x) = 3\times2x = 6x$.

Dérivée d'un produit

Si $u$ et $v$ sont deux fonctions dérivables sur un intervalle $I$ de  $\mathbb{R}$ alors $u\times v$ est dérivable sur $I$ et on a :

$(u\times v)' = u'\times v + u\times v'$.

Exemple :

$f(x) = 3{x}^2(5x + 2)$$u(x) = 3{x}^2$, $u'(x) = 6x$. $v(x) = 5x + 2$, $v'(x) = 5$. $f '(x) = 6x(5x + 2) + 5\times3{x}^2 = 45{x}^2 + 12x$.

Dérivée d'une fonction rationnelle

Si $u$ et $v$ sont deux fonctions dérivables sur un intervalle $I$ et si $v(x) \neq 0$ pour tout $x$ de $I$ alors $\frac{u}{v}$ est dérivable sur $I$ et on a :

$(\frac{u}{v})' = \frac{u' v - u v'}{{v}^2}$.

Exemple :

$f(x) = \frac{3{x}^2}{5x + 2}$. $u(x) = 3{x}^2$, $u'(x) = 6x$. $v(x) = 5x + 2$, $v '(x) = 5$.$f '(x) = \frac{6x(5x + 2) - 5\times 3{x}^2}{{(5x + 2)}^2}$.

1) Bijection et application réciproque

Soit $A$ et $B$ deux parties de ${\Bbb R}$. Une bijection de $A$ dans $B$ est une fonction de $A$ dans $B$ tel que tout élément de $B$ admet un unique antécédent par $f$ dans $A$. 

Si une $f$ est une bijection, on peut alors définir l'application réciproque $f^{-1}$ de $B$ dans $A$ qui a $y$ de $B$ associe son unique antécédent. 

Exemple :

La fonction $f$ de ${\Bbb R}^+$ dans ${\Bbb R}$ définie par $f(x)=x^2$ n'est pas bijective car $-1$ (par exemple n'a pas d'antécédent). 

La fonction $g$ de ${\Bbb R}$ dans ${\Bbb R}^+$ définie par $g(x)=x^2$ n'est pas bijective car $9$ a deux antécédents qui sont $3$ et $-3$. 

La fonction $h$ de ${\Bbb R}^-$ dans ${\Bbb R}^+$ définie par $h(x)=x^2$ est bijective. Son application réciproque est l'application $h^{-1}: {\Bbb R}^+ \longrightarrow {\Bbb R}^-$ définie par $h^{(-1)}(y) = -\sqrt{y}$.

Théorème :

Une fonction d'un intervalle $I$ dans ${\Bbb R}$ strictement monotone et continue est bijective. La réciproque est fausse. 

Exemple :

La fonction suivante est bijective. Mais elle n'est ni strictement monotone ni continue.

Théorème :

Le graphe de l'application réciproque se déduit du graphe de $f$ par une symétrie par rapport à la première bissectrice c'est-à-dire la droite d'équation $y=x$. 

Soit $f$ est une application bijective de $I$ dans $J$ ($I$ et $J$ des intervalles de ${\Bbb R}$). Si $f$ est continue et (par exemple) strictement croissante alors l'application réciproque $f^{-1}$ de $J$ dans $I$ est aussi continue et strictement croissante. 

En revanche, si $f$ est dérivable en un point $x_0$, $f^{-1}$ n'est pas nécessairement dérivable en $y_0=f(x_0)$.

2) Applications trigonométriques réciproques

a) La fonction $\cos$ est une bijection de l'intervalle $[0,\pi]$ dans $[-1,1]$ car c'est une application continue et strictement décroissante. L'application réciproque s'appelle la fonction $\arccos$. Donc l'application $\arccos$ va de $[-1,1]$ dans $[0,\pi]$. 

Par définition, si $x$ dans $[-1,1]$, $\arccos(x)$ est égal à l'angle $\theta$ compris entre $0$ et $\pi$ tel que $\cos(\theta) = x$. 

Exemple :

$\displaystyle{\arccos\left(\frac{1}{2}\right) = \frac{\pi}{3}}$ car d'une part $\displaystyle{\frac{\pi}{3}} \in [0,\pi]$ et d'autre part $\displaystyle{\cos\left(\frac{\pi}{3}\right) = \frac{1}{2}}$.

Graphe de $\arccos$ :

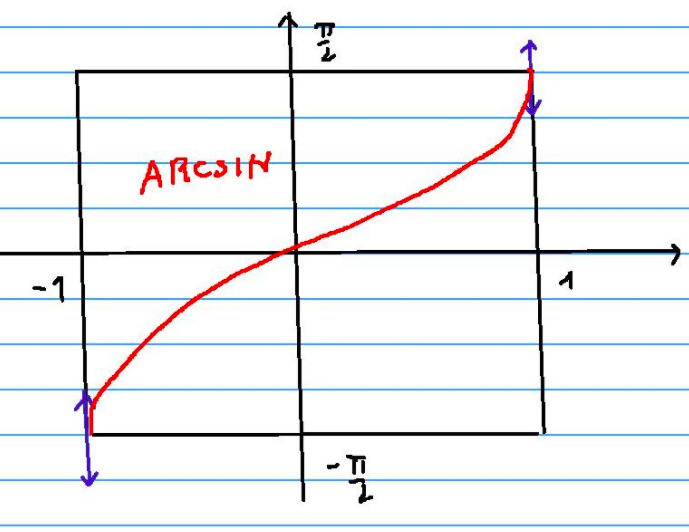
b) La fonction $\sin$ est une bijection de l'intervalle $\displaystyle{\left[-\frac{\pi}{2},\frac{\pi}{2}\right]}$ dans $[-1,1]$ car c'est une application continue et strictement croissante. L'application réciproque s'appelle la fonction $\arcsin$. Donc l'application $\arcsin$ va de $[-1,1]$ dans $\displaystyle{\left[-\frac{\pi}{2},\frac{\pi}{2}\right]}$. 

Par définition, si $x$ dans $[-1,1]$, $\arcsin(x)$ est égal à l'angle $\theta$ compris entre $\displaystyle{-\frac{\pi}{2}}$ et $\displaystyle{\frac{\pi}{2}}$ tel que $\sin(\theta) = x$. 

Exemple :

$\displaystyle{\arcsin\left(-\frac{\sqrt{2}}{2}\right) = -\frac{\pi}{4}}$ car d'une part $\displaystyle{-\frac{\pi}{4}} \in \left[-\frac{\pi}{2},\frac{\pi}{2}\right]$ et d'autre part $\displaystyle{\sin\left(-\frac{\pi}{4}\right) = -\frac{\sqrt{2}}{2}}$.

Graphe de $\arcsin$ :

Propriété : la fonction $\arcsin$ est impaire.

c) La fonction $\tan$ est une bijection de l'intervalle $\displaystyle{\left]-\frac{\pi}{2},\frac{\pi}{2}\right[}$ dans ${\Bbb R}$ car c'est une application continue et strictement croissante. L'application réciproque s'appelle la fonction $\arctan$. Donc l'application $\arctan$ va de ${\Bbb R}$ dans $\displaystyle{\left]-\frac{\pi}{2},\frac{\pi}{2}\right[}$. 

Par définition, si $x$ dans ${\Bbb R}$, $\arctan(x)$ est égal à l'angle $\theta$ compris strictement entre $\displaystyle{-\frac{\pi}{2}}$ et $\displaystyle{\frac{\pi}{2}}$ tel que $\tan(\theta) = x$. 

Exemple :

$\displaystyle{\arctan\left(\sqrt{3}\right) = \frac{\pi}{3}}$ car d'une part $\displaystyle{\frac{\pi}{3}} \in \left]-\frac{\pi}{2},\frac{\pi}{2}\right[$ et d'autre part $\displaystyle{\tan\left(\frac{\pi}{3}\right) = \sqrt{3}}$.

Graphe de $\arctan$ :

Propriété : la fonction $\arctan$ est impaire.

La fonction $\arctan$ a deux asymptotes horizontales d'équations $\displaystyle{x=\pm\frac{\pi}{2}}$.

d) Formules de simplification :

• $\forall x \in [-1,1]$, $\cos(\arccos(x)) = x$ et $\sin(\arcsin(x)) = x$.
• $\forall x \in {\Bbb R}$, $\tan(\arctan(x)) = x$
• $\forall x \in [0,\pi]$, $\arccos(\cos(x)) = x$
• $\displaystyle{\forall x \in\left[-\frac{\pi}{2},\frac{\pi}{2}\right]}$, $\arcsin(\sin(x)) = x$
• $\displaystyle{\forall x \in\left]-\frac{\pi}{2},\frac{\pi}{2}\right[}$, $\arctan(\tan(x)) = x$
• $\forall x \in [-1,1]$, $\sin(\arccos(x)) = \sqrt{1-x^2}$ et $\cos(\arcsin(x)) = \sqrt{1-x^2}$.

e) Dérivée

Les fonctions $\arccos$ et $\arcsin$ sont dérivables sur $]-1,1[$ et $\forall x \in ]-1,1[$, $\arccos'(x) = -\frac{1}{\sqrt{1-x^2}}$ et $\arcsin'(x) = \frac{1}{\sqrt{1-x^2}}$.

La fonction $\arctan$ est dérivable sur ${\Bbb R}$ et $\forall x \in {\Bbb R}$, $\arctan'(x) = \frac{1}{1+x^2}$.

3) Applications hyperboliques réciproques

a) La fonction ${\rm ch}$ est une bijection de l'intervalle ${\Bbb R}^+$ dans $[1,+\infty[$ car c'est une application continue et strictement croissante. L'application réciproque s'appelle la fonction ${\rm argch}$. Donc l'application ${\rm argch}$ va de $[1,+\infty[$ dans ${\Bbb R}^+$. 

Par définition, si $x$ dans $[1,+\infty[$, ${\rm argch}(x)$ est égal au réel $y \ge 0$ tel que ${\rm ch}(y)=x$. 

Par exemple, ${\rm argch}(1) =0$ car ${\rm ch}(0)=1$.

b) La fonction ${\rm sh}$ est une bijection de ${\Bbb R}$ dans ${\Bbb R}$ car c'est une application continue et strictement croissante. L'application réciproque s'appelle la fonction ${\rm argsh}$. Donc l'application ${\rm argsh}$ va de ${\Bbb R}$ dans ${\Bbb R}$. 

Par définition, si $x$ est un réel, ${\rm argsh}(x)$ est égal au réel $y$ tel que ${\rm sh}(y)=x$. 

Par exemple, ${\rm argsh}(0) =0$ car ${\rm sh}(0)=0$.

Propriété : la fonction ${\rm argsh}$ est impaire.

c) La fonction ${\rm th}$ est une bijection de ${\Bbb R}$ dans l'intervalle $]-1,1[$ car c'est une application continue et strictement croissante. L'application réciproque s'appelle la fonction ${\rm argth}$. Donc l'application ${\rm argth}$ va de $]-1,1[$ dans ${\Bbb R}$. 

Par définition, si $x \in ]-1,1[$, ${\rm argth}(x)$ est égal au réel $y$ tel que ${\rm th}(y)=x$. 

Par exemple, ${\rm argth}(0) =0$ car ${\rm th}(0)=0$.

Propriété : la fonction ${\rm argth}$ est impaire.

La fonction ${\rm argth}$ a deux asymptotes horizontales d'équations $\displaystyle{x=\pm1}$.

4) Formule de Taylor et équivalent

Si $f$ est une application suffisamment dérivable, on dispose d'une formule appelée la formule de Taylor-Young qui donne un développement limité de $f$ au voisinage d'un point c'est-à-dire une approximation polynomiale. 

$\displaystyle{f(x_0+h) = \sum_{k=0}^n\frac{f^{(k)}(x_0)}{k!}h^k + h^n\epsilon(h)}$ avec $\displaystyle{\lim_{h \rightarrow 0}\epsilon(h) =0}$. 

Le premier terme non nul de la formule donne un équivalent de la fonction en $x_0$.

Exemple : Déterminer un équivalent de $\displaystyle{f(x) = \arctan(x) - \frac{\pi}{4}}$ au voisinage de $x_0=1$.

Utilisons la formule de Taylor-Young à l'ordre $1$ c''est-à-dire $n=1$.

$\displaystyle{f\left(1+h\right) = f\left(1\right) + f'(0)h + h\epsilon(h)}$.

Or :

$f(1)=0$ et $\displaystyle{f'(x) = \frac{1}{1+x^2}}$ donc $\displaystyle{f'(1)= \frac{1}{2}}$.

Donc :

$\displaystyle{f\left(1+h\right) = \frac{h}{2} + h\epsilon(h)}$. 

On en déduit que :

$\displaystyle{f\left(1+h\right) \stackrel{h \rightarrow 0}{\sim} \frac{h}{2}}$. 

Ou en posant :

$\displaystyle{x=1+h}$, 

On en déduit que :

$\displaystyle{f\left(x\right) \stackrel{x \rightarrow 1}{\sim} \frac{x-1}{2}}$.