Tests du Khi-deux
- Test du Khi-deux d’ajustement d’une distribution expérimentale à une distribution théorique (1 population, 1 caractère)
On considère une distribution expérimentale (observée) d’effectif $N$. On souhaite savoir si la distribution expérimentale est conforme à une distribution théorique.
On suppose que le caractère étudié possède $n$ modalités.
On note $O_i$ l’effectif observé pour la classe de modalité $i$.
D’après la distribution théorique, il y a une probabilité $P_i$ pour qu’un individu présente le caractère correspondant à la modalité $i$.
On appelle $T_i=N\times P_i$ l’effectif théorique pour chaque modalité $i$.
Remarques :
- Un effectif théorique n’est pas toujours un nombre entier mais on n’arrondit pas le résultat afin que les calculs soient le plus précis possible.
On doit retrouver $\displaystyle\sum_{i=1}^n T_i=N$. Il faut donc dans certains cas rajouter des classes supplémentaires pour les calculs d’effectifs théoriques correspondant à des classes pour lesquelles aucune valeur n’avait été observée dans l’échantillon.
Principe du test du $\chi^2$ de Pearson (ici test d’ajustement = test de conformité = test d’adéquation) :
Pour effectuer un test du $\chi^2$, il faut vérifier des conditions d’utilisation : $N\geq 30$, $n_i\geq 5$ pour tout $i$ où $n_i$ représente les effectifs de classe.
Si $n_i<5$, il faut regrouper des classes.
$\nu=n’-1$ indique le nombre de degrés de liberté du test avec $n’$ le nombre de classes après regroupement éventuel.
- $H_0$ : « Il y a conformité entre la distribution expérimentale et la distribution théorique »
- $\chi^2=\displaystyle\sum_{i=1}^n\frac{(O_i-T_i)^2}{T_i}$
- On conclut au risque $\alpha$ en lisant $\chi^2_0$ dans la table du $\chi^2$ de Pearson (avec comme paramètres $\nu$ et $\alpha$).
- Si $\chi^2< \chi^2_0$ on ne rejette pas $H_0$
- Sinon on rejette $H_0$.
Remarque : Pour $\alpha$=5% et ddl=1, $\chi^2_0=3,84$.
Equivalence avec le test « z » :
En notant $p$ la proportion observée sur un échantillon de taille $n$ et $\pi_ {th}$ la proportion théorique, il y a équivalence entre un test « z » de comparaison proportion observée/proportion théorique et un test du Khi-deux de conformité à 1 ddl avec :
$O_1=n\times p$, $O_2=n\times (1-p)$
$T_1=n\times \pi_{th}$, $T_2=n\times (1-\pi_{th})$
- Test du Khi-deux d’association entre caractères qualitatifs (1 population, 2 caractères)
On considère une population qui possède 2 caractères qualitatifs $A$ et $B$ qui peuvent posséder plusieurs modalités : $A_j$ et $B_i$.
On obtient le tableau de contingence suivant avec $O_{ij}$ les effectifs observés :
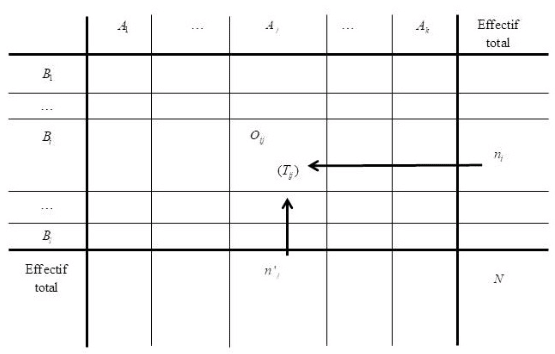
Les effectifs théoriques (indiqués ici entre parenthèses) se calculent de la façon suivante: $T_{ij}=\displaystyle\frac{n_i\times n’_j}{N}$
$\nu=(k-1)(l-1)$ représente le nombre de degrés de liberté du test.
Principe du test du $\chi^2$ de Pearson (ici test d’indépendance) :
Pour effectuer le test, il faut vérifier des conditions d’utilisation : $N\geq 30$, $n\geq 5$ où $n$ représente les effectifs de classe.
$\chi^2=\displaystyle\sum_{i=1}^l\sum_{j=1}^k\frac{(O_{ij}-T_{ij})^2}{T_{ij}}$
Si $ 30\leq N<50$ et $n<5$ on utilise la formule avec la correction de Yates (elle n’est valable que pour les tableaux $2\times 2$) : $\chi^2=\displaystyle\sum_{i=1}^2\sum_{j=1}^2\frac{(|O_{ij}-T_{ij}|-0,5)^2}{T_{ij}}$
- $H_0$ : « Il y a indépendance entre les caractères $A$ et $B$ »
- On conclut au risque $\alpha$ en lisant $\chi^2_0$ dans la table du $\chi^2$ de Pearson (avec comme paramètres $\nu$ et $\alpha$).
- Si $\chi^2< \chi^2_0$ on ne rejette pas $H_0$
- Sinon on rejette $H_0$.
