Soit un repère R d'origine un point O fixe et de base cartésienne B=(→x,→y,→z). Soit un point M de l'espace, alors le vecteur →OM est appelé vecteur position du point M dans ce repère R. Suivant la base de vecteurs adoptée (elle n'est pas toujours cartésienne), ce vecteur peut s'écrire de plusieurs manières.
En base cartésienne
La base est centrée sur le point O qui est fixe, le vecteur →OM s'exprime dans la base cartésienne de cette manière:
→OM=x→x+y→y+z→z
La figure ci-dessous montre la position du point M dans la base cartésienne:

En base cylindrique
La base est centrée sur le point M mobile, le vecteur →OM s'exprime dans la base cylindrique de cette manière:
→OM=r→ur+z→z
La figure ci-dessous montre la position du point M dans la base cylindrique:
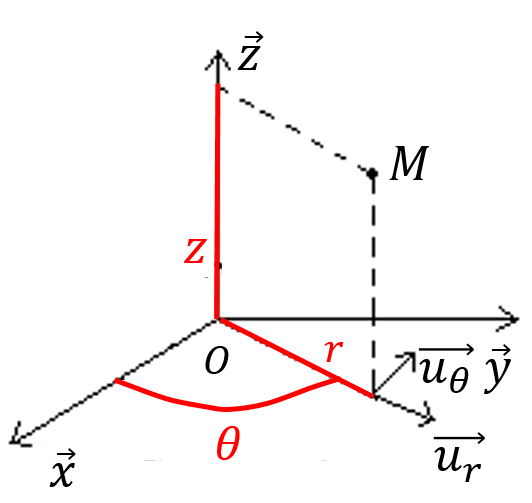
En base cylindrique les vecteurs →ur et →uθ sont facilement exprimables en fonction de la base fixe:
→ur=cos(θ)→x+sin(θ)→y et →uθ=−sin(θ)→x+cos(θ)→y
Il est donc facile de dériver ces vecteurs par rapport au temps dans la base fixe.
En base sphérique
La base est centrée sur le point M mobile, le vecteur →OM s'exprime dans la base sphérique de cette manière:
→OM=r→ur
La figure ci-dessous montre la position du point M dans la base cylindrique:

Remarque : Pour obtenir le vecteur vitesse, il suffit de dériver par rapport au temps le vecteur position par rapport à la base fixe B=(→x,→y,→z).



