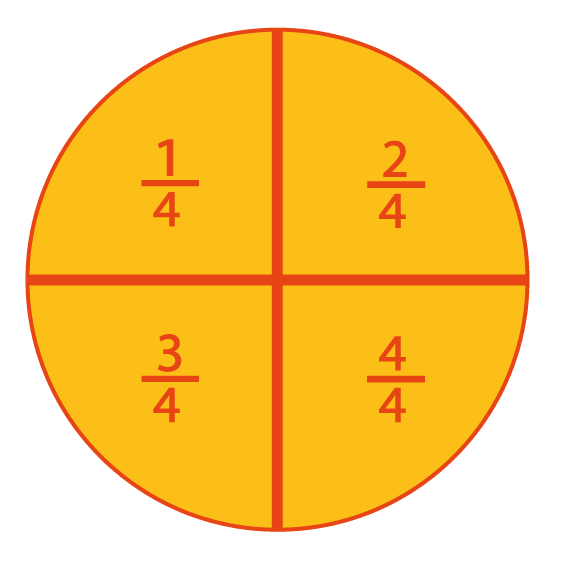
Lorsque l’on partage une unité (bande ou fromage) en parts égales, on obtient des fractions de cette unité (des morceaux de taille égale).
Exemple :
Si on partage une unité en $4$ parts égales, la fraction correspondante est $\displaystyle\frac{1}{4}$ : c’est une part sur quatre.
Dans $\displaystyle\frac{1}{4}$, $1$ est le numérateur. Il indique que l’on a pris une part. $4$ est le dénominateur. Il indique que l’unité est partagée en $4$ parts égales.
- $\displaystyle\frac{1}{2}$ se lit un demi.
- $\displaystyle\frac{1}{3}$ se lit un tiers.
- $\displaystyle\frac{3}{4}$ se lit trois quarts.
- $\displaystyle\frac{1}{10}$ se lit un dixième.
- $\displaystyle\frac{86}{1~000}$ se lit quatre-vingt-six millièmes.
Pour lire les autres fractions, on utilise le suffixe-ième.
Exemple : $\displaystyle\frac{4}{8}$ se lit quatre huitièmes.
Tous les nombres peuvent être écrits sous forme de fractions.
Quand on partage une unité en parts égales, chaque part représente une fraction de cette unité.
Mais une fraction peut représenter une part plus grande que l’unité.
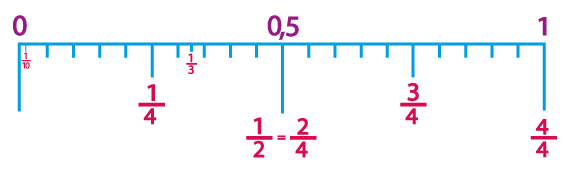
Pour représenter des fractions, on peut les placer sur une droite graduée. Cela permet de les ranger, les comparer et les encadrer entre deux nombres entiers.
Pour encadrer une fraction entre deux nombres consécutifs, on peut soit s’aider d’une droite graduée, soit diviser le numérateur par le dénominateur.
Exemples :
- Pour encadrer $\displaystyle\frac{10}{3}$, $10$ divisé par $3$ n’est pas une opération exacte mais on sait que $3 \times 3 = 9 < 10 < 3 \times 4 = 12$ ; donc on peut écrire $3 < \displaystyle\frac{10}{3} < 4$.
- Pour encadrer une fraction dont le numérateur est plus petit que le dénominateur, ces deux nombres sont toujours $0$ et $1$.
On peut décomposer une fraction sous la forme d’une somme d’un nombre entier et d’une fraction inférieur à $1$.
Exemple : $\displaystyle\frac{17}{4} = \frac{16}{4} + \frac{1}{4} = 4 + \frac{1}{4}$.
