Le théorème du cercle circonscrit

📝 Mini-cours GRATUIT

Périmètres, aires et volumes

Calcul littéral, puissances

Divisions

Transformations géométriques

Aires et volumes

Théorèmes et propriétés de géométrie - 2

Théorèmes et propriétés de géométrie - 1

Proportionnalité - pourcentage - échelle

Proportionnalité et statistiques

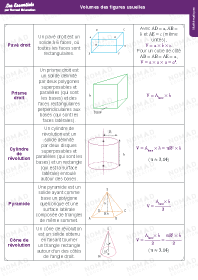
Volumes

Fonctions linéaires et affines

Nombres relatifs et fractions

Nombres et calculs

Triangles et parallélogrammes

Calcul littéral et équations