Opérations

Division

La division de $a$ par $b$ est l'opération qui associe à un nombre $a$ et à un nombre $b$, non nul, un troisième nombre noté $\bf a \div b$ ou $\dfrac{a}{b}$ 

Division euclidienne

Soit $a$ un nombre entier et $b$ un nombre entier non nul. La division euclidienne de $a$ par $b$ est l'opération qui associe à $a$ et à $b$ deux nombres entiers $q$ et $r$ définis par : $a = b \times \bf q + r$ avec $r < b$.

Quand on pose l'opération, on dispose les nombres ainsi :

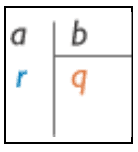
$q$ est le quotient et $r$ est le reste de cette division euclidienne.

Soustraction

La soustraction de $a$ par $b$ est l'opération qui associe, à deux nombres $a$ et $b$, un troisième nombre noté $\bf a - b$.

Priorités opératoires

Distributivité

La multiplication est distributive sur l'addition et la soustraction ; c'est-à-dire que, pour tous nombres $a$, $b$ et $k$, on a :
$k \times (a + b) = k \times a + k \times b$ ; $k \times (a - b) = k \times a - k \times b$.
On a distribué le facteur $\bf k$ sur les termes $\bf a$ et $\bf b$ de la somme et de la différence.

Règles de priorité

Pour calculer une expression numérique sans parenthèses, on effectue les calculs de la gauche vers la droite, en commençant par les multiplications et les divisions qui ont priorité sur les additions et les soustractions.

Si l'expression comprend des parenthèses, on commence par effectuer les calculs à l'intérieur des parenthèses les plus intérieures. On effectue ces calculs en respectant les priorités définies au paragraphe précédent.

Transformations de calcul

Développer une expression

Développer une expression consiste à transformer un produit en une somme algébrique. On utilise la propriété de la distributivité de la multiplication par rapport à l'addition ou à la soustraction.
$\bf k(a + b) = k~a + k~b$
$\bf k(a - b) = k~a - k~b$

Factoriser une expression

Factoriser une expression consiste à transformer une somme algébrique en un produit.
Par exemple, quand on écrit : $\bf k~a + k~b = k(a + b)$ ou $\bf k~a - k~b = k(a - b)$, on a factorisé les expressions $\bf k~a + k~b$ et $\bf k~a - k~b$.
Dans les deux cas, on dit qu'on a mis $k$ en facteur. Le nombre $k$ est appelé un facteur commun.
Ce facteur commun peut être un nombre, une lettre, le produit d'un nombre par une lettre ou une expression entre parenthèses.