Périmètres


Le périmètre d’une figure fermée est la longueur de son contour.

Pour calculer le périmètre d’un polygone, on calcule la somme des longueurs de ses côtés.

Le périmètre d’un rectangle s’exprime en fonction de sa longueur et de sa largeur :

$\rm P = L + \ell + L + \ell$ ainsi ... $\bf P = 2 (L + \ell)$

Le périmètre d’un carré s’exprime en fonction de la longueur de ses côtés.

Ainsi : $\bf P = 4 \times c$

Les mesures de la longueur d’un cercle (la circonférence) font intervenir un nombre noté $\bf \pi$, ce qui se lit « pi », d'une valeur approchée de $3,14$. Le périmètre $\rm P$ d'un cercle de rayon $r$ est donné par la formule $\bf P = 2 \times \pi \times r$.

Aires


Donner l'aire d'une surface, c'est indiquer sa grandeur, son étendue. 

L'aire d'un cylindre de révolution est égale à la somme des aires de ses deux disques de base et de sa surface latérale.

Soit $r$ le rayon d'un disque, l'aire $\bf \mathcal A$ de ce disque est donnée par la formule $\mathcal A = \pi \times r \times r = \pi r^2$ (une valeur approchée du nombre $\pi$ est $3,14$).

Soit $\rm L$, $\ell$ et $h$ les trois dimensions d'un parallélépipède rectangle (pavé droit), l'aire totale $\mathcal A$ de ce solide (celle de ses six faces) est donnée par la formule :

$\mathcal A = 2 \times (L \times \ell + L \times h + \ell \times h)$ ou $\mathcal A = 2\mathrm L\ell + 2\mathrm Lh + 2\ell h$.

Soit $c$ la longueur d'un côté d'un parallélogramme et $h$ celle de la hauteur associée à ce côté, l'aire $\mathcal A$ de ce parallélogramme est donnée par la formule $\mathcal A = c \times h$ ($c$ et $h$ doivent être exprimées dans la même unité).

Soit $c$ la longueur d'un côté d'un triangle et $h$ celle de la hauteur associée à ce côté, l'aire $\mathcal A$ de ce triangle est donnée par la formule $\mathcal A = \dfrac{c \times h}{2}$ ($c$ et $h$ doivent être exprimées dans la même unité).

L'aire $\bf \mathcal A$ d'une sphère de rayon $r$ est donnée par la formule $\bf \mathcal A = 4\pi r^2$ (une valeur approchée du nombre $\pi$ est $3,14$).

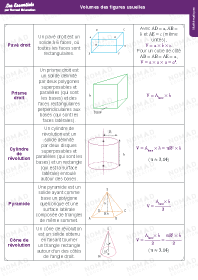
Volumes


Donner le volume d'un solide, c'est indiquer sa grandeur, l'espace qu'il occupe.

Soit un cône de révolution de hauteur $h$ et dont la base a pour aire $\rm B$. Son volume $\rm V$ est donné par la formule :

$\mathrm V = \dfrac{1}{3} \times \mathrm B \times h$

Soit $c$ le côté d'un cube, le volume de ce cube $\rm V$ est donné par la formule :

$\mathrm V = c \times c \times c$.

Soit une pyramide de hauteur $h$ et dont la base a pour aire $\rm B$. Son volume $\rm V$ est donné par la formule :

$\rm V = \dfrac{1}{3} \times B \times h$.

Le volume $\rm V$ d'un prisme droit de hauteur $h$ et ayant une base d'aire $\rm B$ est donné par la formule $\bf V = B \times \mathcal h$.

Le volume $\rm V$ d'une boule de rayon $r$ est donné par la formule $\mathrm V = \dfrac{4}{3}\pi r^3$ (une valeur approchée du nombre $\pi$ est $3,14$).