Monophasé

Les impédances des composants élémentaires

Dipôles composés utilisés en électrotechnique

• Charge inductive
  

Elle se présente sous la forme d'une association série d'une résistance R et d'une inductance L.

Alimentée par une tension alternative sinusoïdale de valeur efficace U, elle est alors traversée par un courant également alternatif sinusoïdal de valeur efficace I donné par la relation :

La tension est déphasée par rapport au courant d'un angle $\varphi$ donné par :

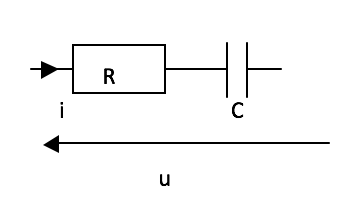
• Charge capacitive
  

Elle se présente sous la forme d'une association série d'une résistance R et d'une capacité C.

Alimentée par une tension alternative sinusoïdale de valeur efficace U, elle est alors traversée par un courant également alternatif sinusoïdal de valeur efficace I donné par la relation : 

La tension est déphasée par rapport au courant d'un angle $\varphi$ donné par :

La construction de Fresnel permet de déterminer des tensions et des courants sinusoïdaux dans le cas où ces courants ou tensions sont déphasés.

L’exemple suivant permet de calculer le courant total i se répartissant à travers les deux charges :

• La charge 1 impose un déphasage $\varphi_1$ entre $\mathrm{i_1~ \text{et} ~u}$.
• La charge 2 impose un déphasage $\varphi_2$ entre $\mathrm {i_2 ~\text{et}~ u}$.
• La tension $\mathrm{u}$ étant commune aux deux charges, c'est elle que l'on prend comme origine des phases.

Afin de déterminer la valeur efficace de $\mathrm{i}$ et le déphasage de $\mathrm{i}$ par rapport à u, on utilise la somme vectorielle :
$$\mathrm {\vec I = \vec I_1 + \vec I_2}$$
La représentation de $\mathrm {\vec I}$ donne :

On projette les trois vecteurs dans un système orthonormé $\mathrm{(O, \vec i, \vec j)}$

$$\mathrm{\vec I_1\left \vert 
\begin{array}{c}
\mathrm{I_{1x} = I_1 \cos \varphi_1} \\
\mathrm{I_{1y} = I_1 \sin \varphi_1}
\end{array}
\right.}$$

$$\mathrm{\vec I_2\left \vert 
\begin{array}{c} 
\mathrm{I_{2x} = I_2 \cos \varphi_2} \\ 
\mathrm{I_{2y} = I_2 \sin \varphi_2}
\end{array} 
\right.}$$

$$\mathrm{\vec I\left \vert 
\begin{array}{c} 
\mathrm{I_{x} = I\cos \varphi} \\ 
\mathrm{I_{y} = I \sin \varphi}
\end{array} 
\right.}$$

On obtient donc : $$\mathrm{I_x = I_1 \cos \varphi_1 + I_2 \cos \varphi_2}$$ et $$\mathrm{I_y = I_1 \sin \varphi_1 + I_2 \sin \varphi_2}$$
La valeur de $\mathrm{I}$ est donnée par : $$\mathrm{I = \sqrt{I_x^2 + I_y^2}}$$
La valeur de $\varphi$ est donnée par : $$\mathrm{\tan \varphi = \frac{I_y}{I_x}}.$$

Les trois puissances $\mathrm{P}$ (puissance active), $\mathrm{Q}$ (puissance réactive) et $\mathrm{S}$ (puissance apparente) peuvent être représentées sous la forme d'un triangle rectangle, duquel les relations entre ces différentes puissances découlent.

$$\mathrm{S = U I} \quad \quad S = \mathrm{\sqrt{P^2 + Q^2}}$$

$$\mathrm{P = U I \cos \varphi = S \cos \varphi}$$

$$\mathrm{Q = U I \sin \varphi = S \sin\varphi} \quad \quad \mathrm{Q = P \tan \varphi}$$

Puissances des dipôles élémentaires et composés

Pour les deux dipôles $\mathrm{RL}$ et $\mathrm{RC}$ présentés précédemment, les puissances active et réactive absorbées s'écrivent :

Lorsque des dipôles sont associés, en parallèle ou en série, chacun d'entre eux consomment de la puissance active et de la puissance réactive. Il s'agit donc, pour connaître la consommation globale de puissance, de recenser les puissances active et réactive de chaque dipôle et de faire la somme des unes et des autres. Le théorème s'énonce donc de la façon suivante :

• La puissance active reçue par une association de dipôles est égale à la somme des puissances actives reçues par chaque dipôle.
• La puissance réactive reçue par une association de dipôles est égale à la somme des puissances réactives reçues par chaque dipôle.
• Les puissances apparentes ne peuvent être additionnées : elles ne se conservent pas.