Dans la République (livre VII), Platon souligne que la géométrie et l’ensemble des disciplines mathématiques sont une étape essentielle de la formation des futurs philosophes :
- L’étude de l’unité montre l’insuffisance d’une réflexion qui s’en tient aux objets sensibles : dans la réalité sensible, rien n’est parfaitement un. Ainsi, Socrate est un en tant qu’individu isolé parmi d'autres, mais il est multiple en tant que corps composé d’éléments divers (Parménide, 129b-130d).
- L’étude des mathématiques entraîne l’intelligence à s’occuper d’objets qui ne sont pas perceptibles par les sens. Lorsqu’on réfléchit sur la définition du triangle, on ne porte pas son regard sur les détails et les particularités d’un triangle sensible, mais sur la notion de triangle elle-même.
Le raisonnement mathématique utilise donc les réalités sensibles (le triangle tracé sur une feuille, qui a une longueur déterminée) comme images de réalités intelligibles (le triangle en soi, qui correspond à la définition même du triangle).
Mais, selon Platon (République VI, 511c), ce raisonnement a comme inconvénient qu’il n’interroge pas certaines notions (comme l’unité, la différence entre le pair et l’impair), mais les utilise comme les points de départ de raisonnements ultérieurs. Les mathématiques n’explorent pas leurs propres principes, mais raisonnent à partir d’hypothèse ininterrogées.
La « dialectique » consiste au contraire à interroger directement ces notions utilisées comme hypothèses et à remonter au « principe anhypothétique » qui les explique ; à partir de ce principe absolu, l’on peut déduire le reste des notions intelligibles.
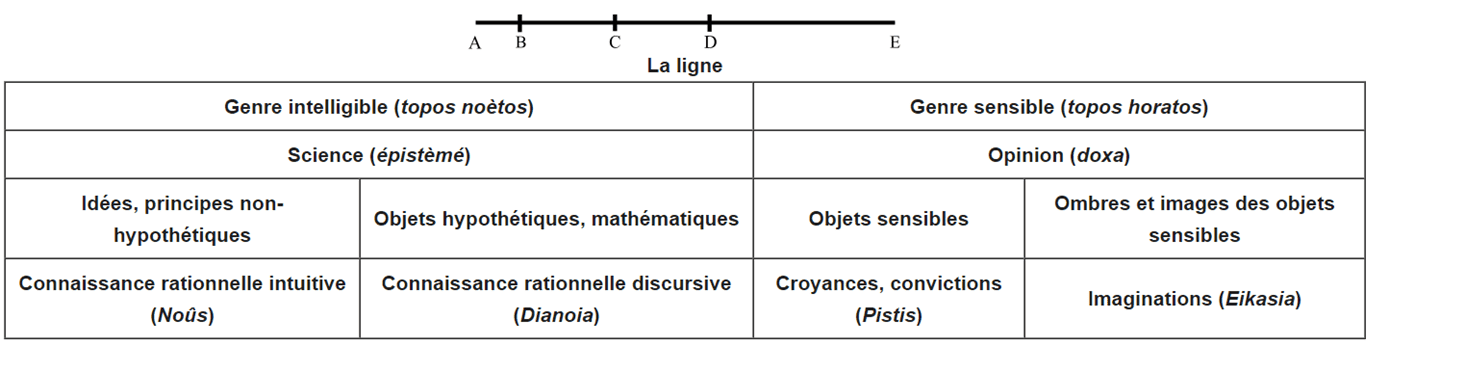
Socrate propose alors une célèbre analogie pour expliquer le rapport des différents objets pensés et des facultés employées pour les penser : il s'agit de diviser une ligne en deux sections d’inégales longueurs :
- la plus grande est composée des réalités sensibles ;
- la plus petite des réalités intelligibles.
Puis, ces deux sections se divisent à leur tour chacune en deux sections inégales :
- la section sensible se divise entre une section composée des réalités corporelles en devenir et une autre des reflets, ombres ou imitations de ces réalités ;
- la section intelligible se divise entre une section composée des réalités mathématiques, qui sont saisies par la dianoia (raisonnement discursif), et une section composée des réalités intelligibles, qui sont saisies par le noûs (intellection intuitive).
Entre chaque section, il existe un rapport de ressemblance, comme entre le modèle et la copie.