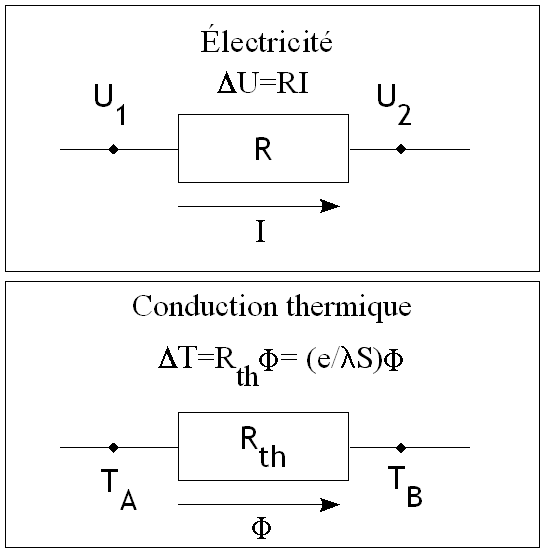
Les modes de transferts thermiques

La conduction thermique : transfert de chaleur direct entre constituants en contact (ce phénomène fait l'objet de ce mini cours).

La convection thermique : transfert de chaleur qui s’effectue grâce à un mouvement de matière dans un milieu liquide ou gazeux. Le courant de convection $\mathrm{j}$ est donné par $\mathrm{j=h(T_{int}-T_{ext})}$ avec $\mathrm{h}$ le coefficient de convection et $\mathrm{T_{int}}$ et $\mathrm{T_{ext}}$ les températures respectivement intérieures et extérieures.

Le rayonnement thermique : transfert d'énergie par intermédiaire d'un champ électromagnétique. Ce phénomène peut être décrit par la loi de Wien.

Flux thermique à travers une surface élémentaire $\vec{dS}$

\[\mathrm{d^2\Phi_{th}=\vec{j_{th}}.\vec{dS}}\]

Loi de Fourier

$\mathrm{\vec{j_{th}}=-\lambda.\vec{grad}(T)}$ avec $\lambda$ la conductivité thermique.

À une dimension on peut écrire :

\[\mathrm{j_{x\: th}=-\lambda \frac{\partial T}{\partial x}}.\]

Équation de la diffusion thermique

Dans le cas où il n'y a aucun processus de création ou de consommation thermique :

$\mathrm{D \Delta T = \frac{ \partial T}{ \partial t}}$ avec $\Delta$ l'opérateur laplacien.

À une dimension on peut écrire :

\[\mathrm{D \frac{ \partial ^2 T}{ \partial x^2} = \frac{ \partial T}{ \partial t}}\]

Avec $\mathrm{D=\frac{\lambda}{\rho.c_p}}$ la diffusivité thermique, avec $\rho$ la masse volumique du matériau étudié et $\mathrm{c_p}$ la capacité thermique massique.

Les modes de transferts thermiques

Flux thermique à travers une surface élémentaire $\vec{dS}$

Loi de Fourier

Équation de la diffusion thermique

Analogie entre diffusion thermique et électricité

Diffusion thermique

📝 Mini-cours GRATUIT

Diffusion thermique

🎲 Quiz GRATUIT

NOMAD EDUCATION

L’app unique pour réussir !

Pour profiter de votre abonnement, rendez-vous dans l’app ou sur le site internet, avec le compte email associé à l’achat