Résistance des matériaux

Modèle de la poutre

Une poutre est un solide déformable ayant les propriétés suivantes:

- Une dimension est très grande devant les 2 autres.
- Le rayon de courbure de la ligne moyenne de la courbe est grand.
- La section droite varie de manière continue le long de la ligne moyenne.

De plus pour les calculs on suppose que l'hypothèse des petites perturbations est respectée et que le matériau de la poutre est linéaire, homogène, isotrope.

Les formules utilisées seront valables loin des points d'application des forces et des liaisons pour respecter le principe de Saint-Venant.

Pour la suite l'hypothèse de Navier-Bernoulli sera appliquée: lors de la déformation de la poutre, les sections normales à la ligne moyenne restent planes.

Torseur de cohésion

On considère une poutre à laquelle on associe un repère fixe $\mathcal{R}=(O,\overrightarrow{x_{0}},\overrightarrow{y_{0}},\overrightarrow{z_{0}})$. On considère une coupe droite $(E)$ de la poutre située à l'abscisse $x$, $S_{x}$ est la surface de la section et $G_{x}$ son centre de gravité. On note $(E_{g})$ et $(E_{d})$ les parties à gauche et à droite de cette coupe et on associe à $G_{x}$ le repère mobile $(O,\overrightarrow{x},\overrightarrow{y},\overrightarrow{z})$ dont $\overrightarrow{x}$ reste tangent à la ligne médiane de la poutre :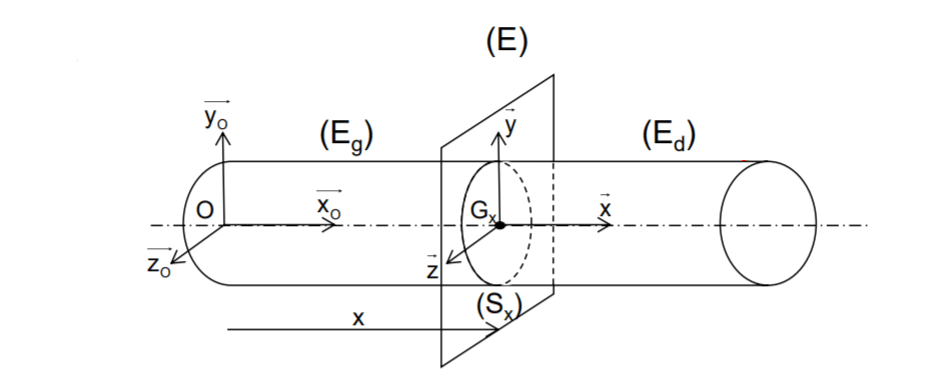



Avec cette convention de repères et en isolant $(E_{g})$ on peut définir le torseur de cohésion exprimé au point $G_{x}$ comme les actions de $(E_{d})$ sur $(E_{g})$:

On considère une poutre à laquelle on associe un repère fixe $\mathcal{R}=(O,\overrightarrow{x_{0}},\overrightarrow{y_{0}},\overrightarrow{z_{0}})$. On considère une coupe droite $(E)$ de la poutre située à l'abscisse $x$, $S_{x}$ est la surface de la section et $G_{x}$ son centre de gravité. On note $(E_{g})$ et $(E_{d})$ les parties à gauche et à droite de cette coupe et on associe à $G_{x}$ le repère mobile $(O,\overrightarrow{x},\overrightarrow{y},\overrightarrow{z})$ dont $\overrightarrow{x}$ reste tangent à la ligne médiane de la poutre :



Il est possible d'évaluer les contraintes au sein de la poutre à partir des actions mécaniques extérieures s'exerçant sur elle.

Poutre en traction-compression

On reprend la poutre précédente (de module de Young $E$) qui subit à l'extrémité droite un effort $\overrightarrow{N}=N\overrightarrow{x_{0}}$. La contrainte en tout point d'une section droite de la poutre s'écrit:

\begin{equation*}
\sigma_{x}=\dfrac{N}{S_{x}}
\end{equation*}

Par convention $N>0$ si la poutre est sollicitée en traction, $N<0$ si la poutre est en compression.

Poutre en flexion

On suppose cette fois que la poutre précédente subit un effort $F\overrightarrow{y_{0}}$ à son extrémité droite, cela crée alors un moment de flexion $\overrightarrow{M_{fz}}$ autour de l'axe $\overrightarrow{z_{0}}$. On note $y$ l'ordonnée d'une section droite située en $x$ et centrée en $G_{x}$. La contrainte longitudinale s'exprime alors:

\begin{equation*}
\sigma_{x}=-\dfrac{M_{fz}}{I_{z}}y
\end{equation*}

La contrainte est positive sur la zone étirée, négative sinon. Il n'y a pas de contrainte le long de la fibre neutre.

Poutre en torsion

Pour ce cas d'étude la poutre a une section droite circulaire de rayon $R$, on applique à son extrémité droite un moment de torsion $M_{t}\overrightarrow{x_{0}}$. Sur une tranche de poutre de longueur $dx$ il est possible d'observer 2 angles: l'angle $d\varphi$ de rotation de la section de centre $G_{x}$ et l'angle $\gamma$ de distorsion comme le montre la figure ci-dessous.



Ces 2 angles sont liés par la relation suivante, toujours dans l'hypothèse des petites perturbations:

\begin{equation*}
\gamma = r\dfrac{d\varphi}{dx}
\end{equation*}

$r$ est la distance radiale entre le centre $G_{x}$ de la section et un point de cette section, il est compris entre $0$ et $R$. Le cisaillement $\tau$ est proportionnel à $\gamma$ et s'écrit:

\begin{equation*}
\tau=G\gamma = G.r\dfrac{d\varphi}{dx}
\end{equation*}

Où $G$ est le module de cisaillement $G=\dfrac{E}{1+\nu}$ pour la poutre isotrope. Enfin il est possible de lier $\tau$ au moment de torsion $M_{t}(x)$, au moment quadratique $I_{x}$ et au rayon $r$:

\begin{equation*}
\tau=r\dfrac{M_{t}(x)}{I_{x}}
\end{equation*}

Le cisaillement est nul sur la ligne médiane de la poutre et maximum à $r=R$.