Action Mécanique (abréviation A.M.)
C'est un phénomène physique qui peut engendrer :
- Un déplacement (modification de sa trajectoire ou de sa vitesse)
- Le maintien d'un corps en équilibre
- La déformation d'un corps
On en recense 2 types :
- L' A.M. de contact (en un point ou sur une surface), exercées par le contact entre 2 solides.
- L' A.M. à distance ou volumique, qui s'applique sur tout le volume du solide sans contact (ex : action de la pesanteur).
La modélisation et l’étude des mécanismes est réalisée grâce aux champs suivants :
· La statique permet de calculer les efforts mis en jeu.
· La cinématique permet d’étudier les mouvements relatifs de ses composants
· La dynamique permet de calculer les puissances transmises.
Rappels
Force
C'est une A.M. qu'exerce un solide sur un autre solide si leur liaison est de type ponctuelle. Elle est définie par :
- un point d'application : le point de contact entre les 2 solides
- une direction : normale (=perpendiculaire) au plan tangent au contact.
- un sens : du solide A vers le solide A s'il s'agit de l'A.M. de A sur B.
- une intensité : exprimée en Newton (N)
Moment
- Moment d'une force : M=F.d

- Moment d'un couple : M=F.d
La formule est identique mais nous avons un couple de forces (2 forces opposées de même intensité, avec des droites d'action //)

Torseur des actions mécaniques transmissibles (TAMT)
Utilisé dans la vérification des performances d'un mécanisme (Voir ci-dessous : P.F.S. & P.F.D.).
On étudie les actions d'un solide S1 sur un solide S2 :
{T1→2}A={→R(1→2)→MA(1→2)}A
A est le point d'application de la force.
{T1→2}B={XLYLZN}B,R
Forme d'écriture décomposée dans le repère. B est le point de réduction du torseur.Chaque liaison a donc son propre TAMT en fonction de ses caractéristiques.
Principe Fondamental de la Statique
La statique est l'étude d'un système S isolé de son environnement Sext qui est en équilibre (pas de mouvement).
Si S est en équilibre, le torseur résultant des A.M. de Sext sur S est égal au torseur nul.
{TSext→s}P={→0→0}P
⇒ La résultante des A.M. est nulle : →RSext→S=→0
⇒ Le moment résultant en un point P des A.M. est nul : MP(Sext→S)=→0
Principe des interactions
Soient S1 et S2, deux systèmes matériels en équilibre : {TS1→S2}P=−{TS2→S1}P
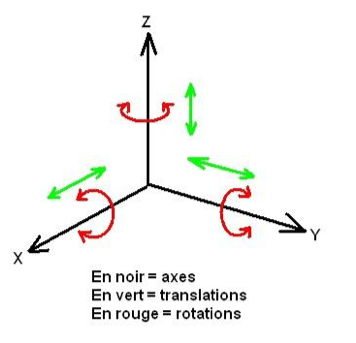
Mobilités, degrés de liberté et de liaison
Un système mécanique est l'association de plusieurs solides qui ont des liaisons donc des degrés de liberté les uns par rapport aux autres.
Les constituants doivent être assemblés en respectant certaines conditions qui déterminent leurs possibilités de mouvements relatifs, c'est à dire leurs degrés de liberté.
Dans tous les cas, dans une liaison entre deux pièces :
Nombre de degrés de liberté + Nbre degrés de liaison = 6