Définition
L’unique fonction f définie et dérivable sur R vérifiant f′=f et f(0)=1 est la fonction exponentielle.
Elle est notée x↦exp(x)=ex.
Propriétés algébriques
e0=1
Pour tous nombres réels x et y :
ex+y=ex×ey ;
e−x=1ex ;
ex−y=exey ;
(ex)n=enx (n entier naturel).
Fonction exponentielle
📝 Mini-cours GRATUIT
Exponentielle 2
Propriétés graphiques
La fonction exponentielle est définie, dérivable, strictement croissante et strictement positive sur l'ensemble des nombres réels.
La fonction exponentielle est sa propre dérivée.
Représentation graphique
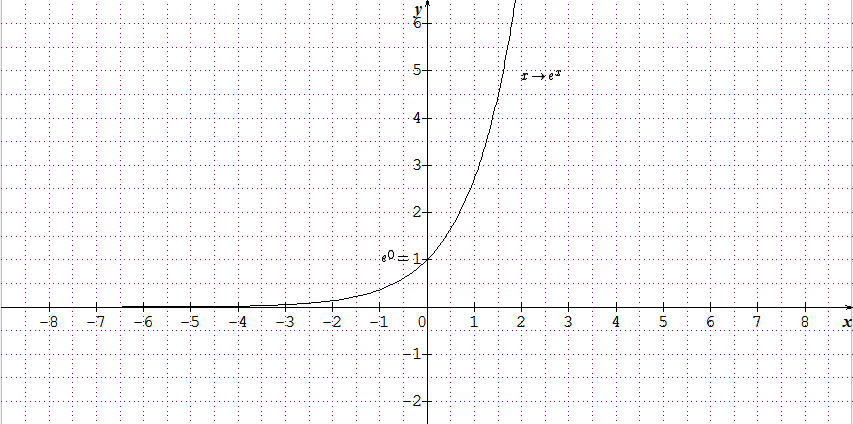
Exponentielle 3
Suites $({\mathrm{e}}^{na})$ ($a$ réel)
Pour $a$ un nombre réel, la suite $({\mathrm{e}}^{na})$ définie sur $\mathbb{N}$ est une suite géométrique.
En effet, pour tout nombre réel $a$ et tout entier naturel $n$, $({\mathrm{e}}^{na}) = {({\mathrm{e}}^a)}^n$.
Pour tout entier naturel $n$, nous avons donc :
${\mathrm{e}}^{(n+1)a} = {({\mathrm{e}}^a)}^{n+1}= {({\mathrm{e}}^a)}^n \times {\mathrm{e}}^a = {\mathrm{e}}^a \times {({\mathrm{e}}^a)}^n = {\mathrm{e}}^a \times {\mathrm{e}}^{na}.$
La suite $({\mathrm{e}}^{na})$ définie sur $\mathbb{N}$ est donc une suite géométrique de raison ${\mathrm{e}}^a$ (qui ne dépend pas de $n$) et de premier terme ${\mathrm{e}}^0 = 1$.
Fonctions $t \mapsto {\mathrm{e}}^{-kt}$ et $t\mapsto {\mathrm{e}}^{kt}$ ($k > 0$)
Pour $k > 0$ un nombre réel fixé.
La fonction $t\mapsto {\mathrm{e}}^{kt}$ est définie, strictement croissante (croissance exponentielle) et positive sur l'ensemble des nombres réels.
La fonction $t\mapsto {\mathrm{e}}^{-kt}$ est définie, strictement décroissante (décroissance exponentielle) et positive sur l'ensemble des nombres réels.
Exemples de représentations graphiques :

📺 Vidéos GRATUIT
📄 Exos type bac PREMIUM

Fonction exponentielle 1

Dérivation, variations et courbes représentatives des fonctions 1
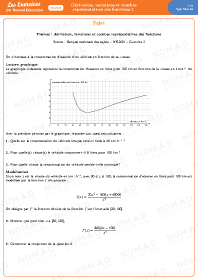
Dérivation, variations et courbes représentatives des fonctions 2
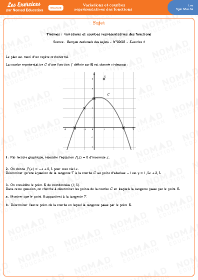
Variations et courbes représentatives des fonctions

Fonction exponentielle, Fonction trigonométrique, etc.

Dérivation, variations et courbes représentatives des fonctions 2

Dérivation, Fonctions trigonométriques, géométrie repérée, etc.

Fonction exponentielle, calcul vectoriel et produit scalaire, etc.
📄 Annale PREMIUM

Sujet zéro — Spécialité Mathématiques
🍀 Fiches de révision PREMIUM

Fonctions exponentielles et fonctions associées

Formulaire d’analyse




