Valeurs remarquables
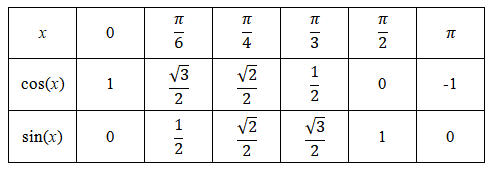
Cosinus et sinus d’angles associés
Pour tout nombre réel :
;
;
;
;
Pour tout nombre réel :
;
;
;
.
Valeurs remarquables

Cosinus et sinus d’angles associés
Pour tout nombre réel :
;
;
;
;
Pour tout nombre réel :
;
;
;
.
Fonction cosinus
La fonction cosinus est définie sur R.
Elle est périodique de période 2π et sa représentation graphique (en bleu) est une sinusoïde de période 2π.
La fonction cosinus est paire donc sa représentation graphique est symétrique par rapport à l'axe des ordonnées.
Fonction sinus
La fonction sinus est définie sur R.
Elle est périodique de période 2π et sa représentation graphique (en noir) est une sinusoïde de période 2π.
La fonction sinus est impaire donc sa représentation graphique est symétrique par rapport à l'origine du repère.


Fonction exponentielle 1

Dérivation, variations et courbes représentatives des fonctions 1
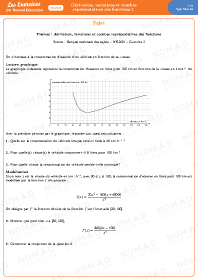
Dérivation, variations et courbes représentatives des fonctions 2
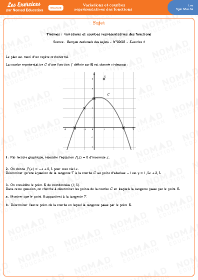
Variations et courbes représentatives des fonctions

Fonction exponentielle, Fonction trigonométrique, etc.

Dérivation, variations et courbes représentatives des fonctions 2

Dérivation, Fonctions trigonométriques, géométrie repérée, etc.

Fonction exponentielle, calcul vectoriel et produit scalaire, etc.

Sujet zéro — Spécialité Mathématiques

Fonctions trigonométriques

Formulaire d’analyse



