La forme de la Terre
📝 Mini-cours GRATUIT
🍀 Fiches de révision PREMIUM

Physique-Chimie / La matière

SVT / L'énergie solaire et la photosynthèse
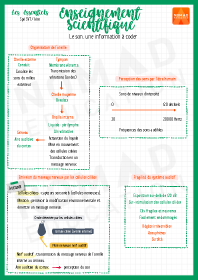
SVT / Le son, une information à coder

Physique-Chimie / Se repérer sur Terre
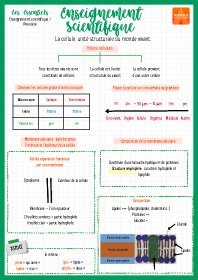
SVT / La cellule, unité structurale du monde vivant
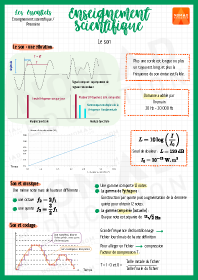
Physique-Chimie / Le son
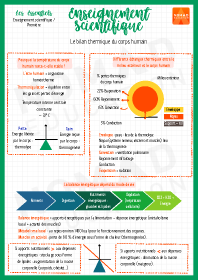
SVT / Le bilan thermique du corps humain
Physique-Chimie / Énergie



