Types et valeurs de base
📝 Mini-cours GRATUIT
Notation à position et bases de numération
La base deux
La base seize
Notion d’octet
La représentation des entiers relatifs en complément à 2
La représentation des nombres à virgule
La représentation des caractères
La représentation des textes
📄 Exos type bac PREMIUM

Exercice 1

Exercice 2

Exercice 3
📄 Annale PREMIUM

Sujet zéro — Numérique et sciences informatiques
🍀 Fiches de révision PREMIUM

Systèmes d'exploitation

Python / Variables
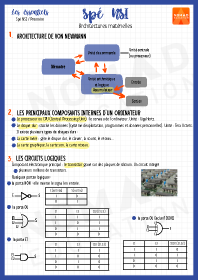
Architectures matérielles

Python : Fonctions – Librairies – Opérateurs booléens

Algorithmes de référence

Python : Structure de contrôle

Représentations des données : types construits
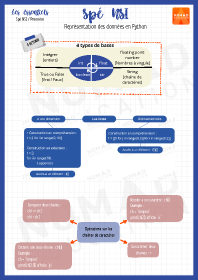
Représentation des données en Python

Spé NSI
📄 Annale PREMIUM

Sujet zéro — Numérique et sciences informatiques



