Interactions fondamentales

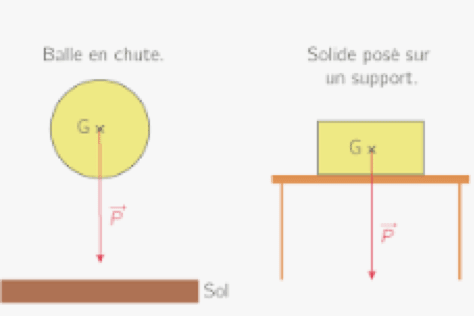
Poids :

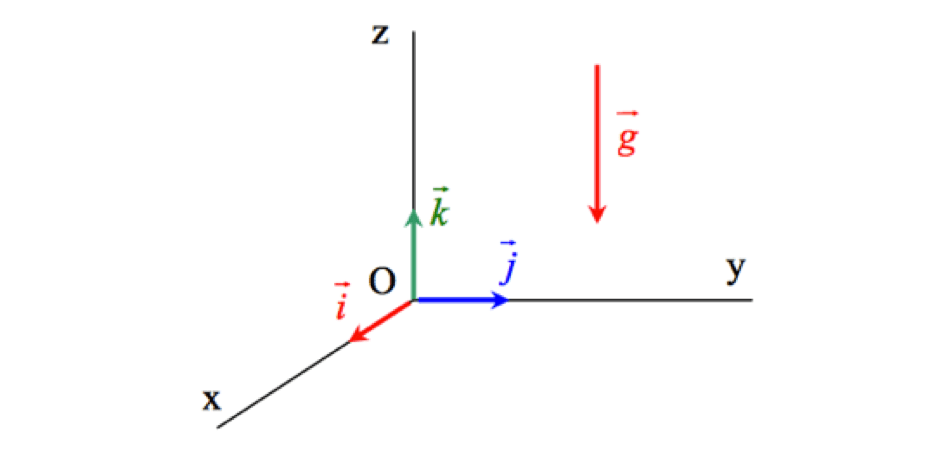
Le poids noté $\rm P$ ayant pour caractéristique son point d’application (centre de gravité de l’objet) ; sa direction (verticale) ; son sens (de l’objet vers le centre de la Terre (vers le bas)) et sa norme $\rm P = m \times g$ avec $\rm P$ le poids en Newton $\rm N$, $\rm m$ masse de l’objet en $\rm kg$ et $\rm g$ intensité de la pesanteur en $\rm N.kg^{-1}$.

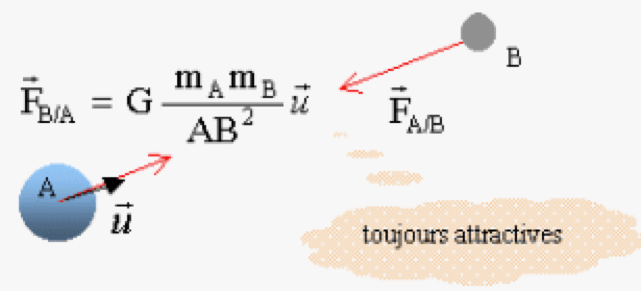
Force de gravitation :

• $\rm F_{A/B}$ et $\rm F_{B/A}$ : force en Newton
• $m_{\mathrm A}$ et $m_{\mathrm B}$ : masses des corps $\rm A$ et $\rm B$ en $\rm kg$
• $d$ : distance entre les deux corps en $m$
• $\rm G$ : constante gravitationnelle

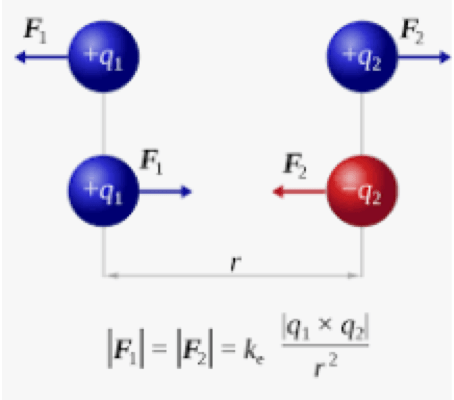
Force électrostatique :

Avec $\rm F$ en Newton $\rm (N)$, $\rm k$ (constante) en $\rm N.m^2.C^{-2}$, $q_1$ et $q_2$ charges en Coulomb$(C)$, $d$ distance entre les corps en $m$.

Poussée d'Archimède :

Principe d'Archimède : tout corps (lâché sans vitesse initiale), plongé dans un fluide homogène subit une force verticale ascendante $\vec \pi_a$ exercée au centre de gravité $\rm G$ du corps considéré égale au poids du volume de fluide déplacé :

$\rho$ étant la masse volumique du fluide et $v$ le volume de fluide déplacé.

Caractéristiques :

• Origine : centre d'inertie $\rm G$ du système.
• Sens : du bas vers le haut.
• Direction : Verticale passant par $\rm G$ et le centre de la Terre.
• Norme : $\pi_a = m_{\rm fluide} \times g = \rho \times v \times g$.

$\pi_a$ s'exprime en newton $\rm (N)$ ; $m_{\rm fluide}$ en $\rm kg$ ou $\rho$ en $\rm kg.m^{3}$ et $v$ en $\rm m^3$ ; $g$ en $\rm N.kg^{-1}$.

Un solide est en chute libre lorsqu'il n'est soumis qu'à l'action de son poids.

Le système étudié est un solide de masse $\rm m$ et de centre d'inertie $\rm G$.
Le poids $\mathrm{\vec P} = m\vec g$ est la seule force qui s'exerce sur ce système : la deuxième loi de Newton permet d'écrire $\displaystyle \mathrm{\sum \overrightarrow{F_{ext}} = \vec P} = m{\overrightarrow{a_\rm G}}$ soit $m\vec g = m\overrightarrow{g} = m{\overrightarrow{a_\rm G}}$ et enfin $\overrightarrow{a_\rm G} = \vec g$.

Le vecteur accélération du centre d'inertie d'un solide lors d'une chute libre est égal au vecteur champ de pesanteur : la valeur de l'accélération ne dépend pas de la masse du solide.

Dans le référentiel terrestre, on choisit un repère d'espace othonormal $(\mathrm O, \vec i, \vec j, \vec k)$ tel que l'axe vertical $(\mathrm O~;\vec k)$ est dirigé vers le haut.

La relation vectorielle $\overrightarrow{a_\rm G} = \vec g$ permet d'écrire les coordonnées du vecteur accélération du centre d'inertie du solide puisqu'on connaît celles de $\vec g$.

\[\overrightarrow{a_\rm G}(t) = \left\{\begin{array}{ll} a_x(t) = 0\\ a_y(t) = 0\\a_z(t) = -g \end{array}\right.\]

Chute libre sans vitesse initiale :

Par définition, l'accélération étant la dérivée de la vitesse, on en déduit les équations différentielles vérifiées par les coordonnées du vecteur vitesse :

\[\left\{\begin{array}{ll}
\displaystyle \frac{dv_x}{dt}  = 0 \\
\displaystyle \frac{dv_y}{dt} = 0 \\
\displaystyle \frac{dv_z}{dt} = -g \\
\end{array}\right.\]

A l'instant de date $t_o$, l'objet est lâché sans vitesse initiale :

\[\mathrm{\overrightarrow{OM}}(t_o) = \mathrm{\overrightarrow{OM_\cal o}}
\left\{\begin{array}{lll}
x(t_o) = 0 \\
y(t_o) = 0 \\
z(t_o) = 0 \\
\end{array}\right.\]

\[\rm et\]

\[\vec v(t_o) = \overrightarrow{v_o}
\left\{\begin{array}{lll}
v_x(t_o) = 0 \\
v_y(t_o) = 0 \\
v_z(t_o) = 0 \\
\end{array}\right.\]

Dans une chute libre sans vitesse initiale, les coordonnées du vecteur vitesse du centre d'inertie vérifient les équations horaires :

\[\vec v(t)
\left\{\begin{array}{lll}
x(t_o) = 0 \\
y(t_o) = 0 \\
z(t_o) = -gt \\
\end{array}\right.\]

La valeur de la vitesse instantanée est donnée par $\displaystyle \sqrt{v_x^2(t) +v_y^2(t) + v_z^2(t)}$.
Dans le cas étudié, nous avons $v(t) = gt$.
Le mouvement rectiligne uniformément varié est qualifié d'uniformément accéléré.

\[\mathrm{\overrightarrow{OM}}(t)
\left\{\begin{array}{lll}
x(t) = 0 \\
y(t) = 0 \\
z(t) = \displaystyle - \frac{1}{2}gt^2 \\
\end{array}\right.\]