Définition
On considère une fonction $f$ dérivable sur l’intervalle $\rm I$.
La fonction $F$ est une primitive de la fonction $f$ sur l'intervalle $\rm I$ si :
pour tout $x\in$I, $F’(x) = f(x)$.
L'ensemble des primitives de la fonction $f$ sur $\rm I$ est composé des fonctions définies sur $\rm I$ par $F(x) + k$ avec $k$ un nombre réel.
Deux primitives d’une même fonction sur un intervalle $\rm I$ diffèrent d’une constante.
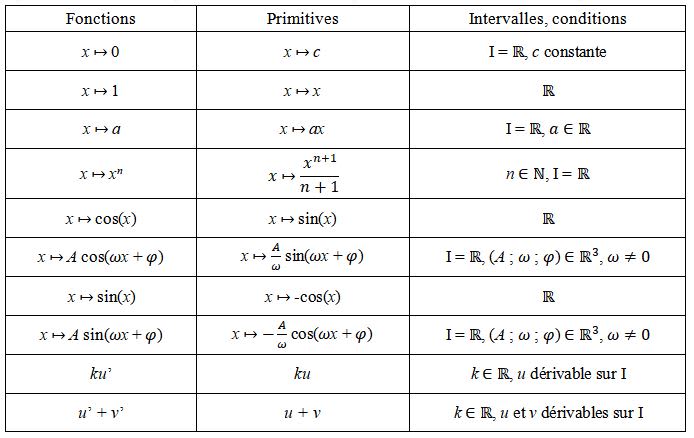
Tableau de primitives
