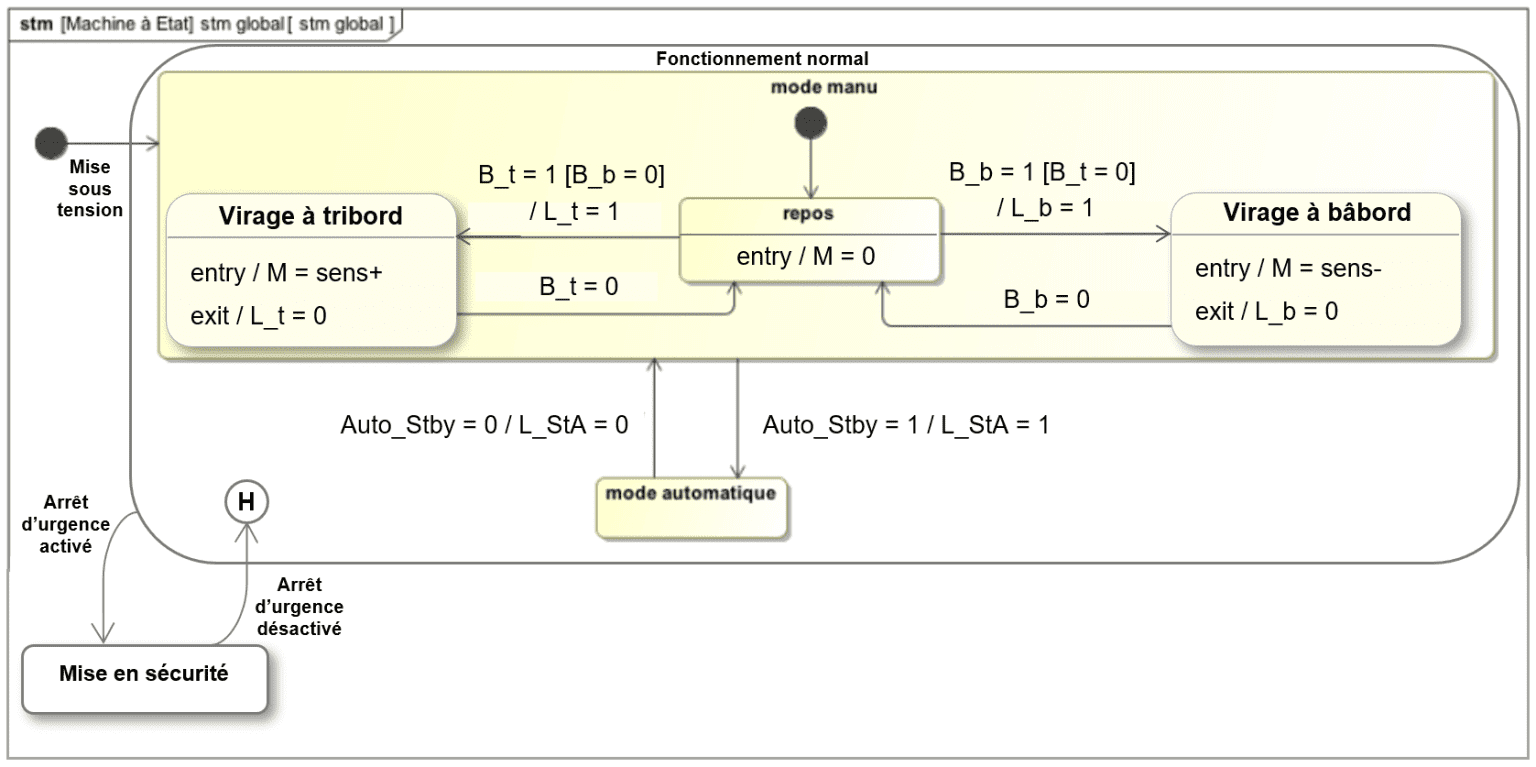
La logique combinatoire est le domaine des systèmes numériques manipulant uniquement des variables logiques (deux états : 1 - VRAI et 0 - FAUX) et dont l’état des sorties ne dépend que de l’état des entrées à l’instant considéré.
Une fonction logique est l’expression d’une variable de sortie logique en fonction d’une ou plusieurs variable(s) d’entrée logique(s). La table de vérité d’une fonction logique recense les différentes combinaisons des valeurs des entrées et indique pour chacune d’elles la valeur de la sortie. Le tableau ci-dessous représente les principales fonctions logiques de base :
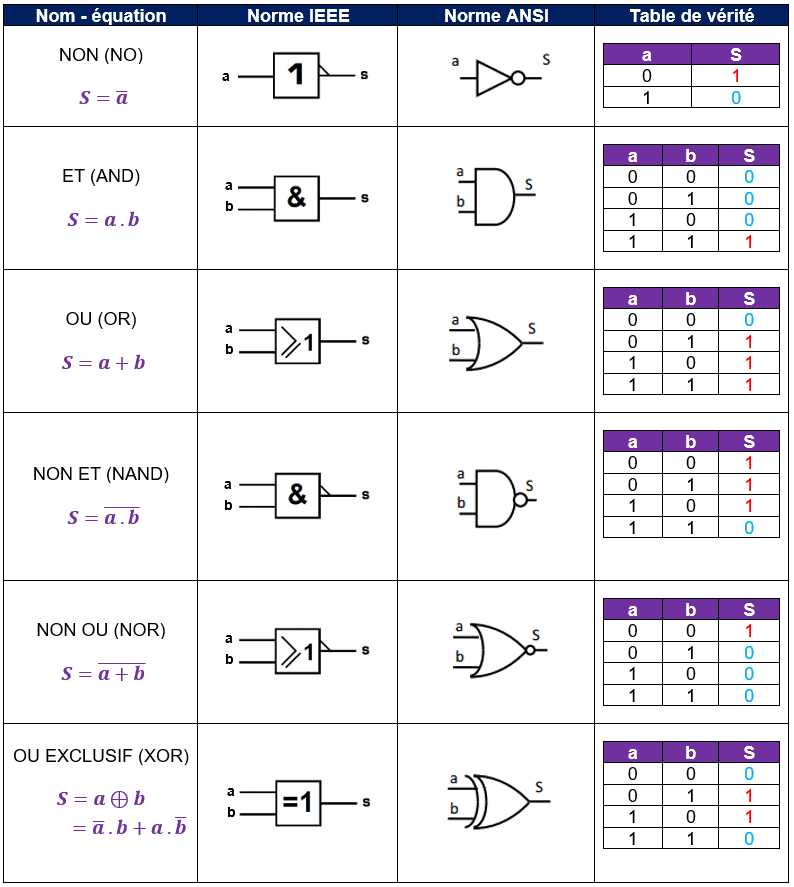
Les fonctions logiques plus complexes (ainsi que, grâce aux portes associées, les circuits électroniques logiques appelés logigrammes) seront construites par association de ces fonctions.
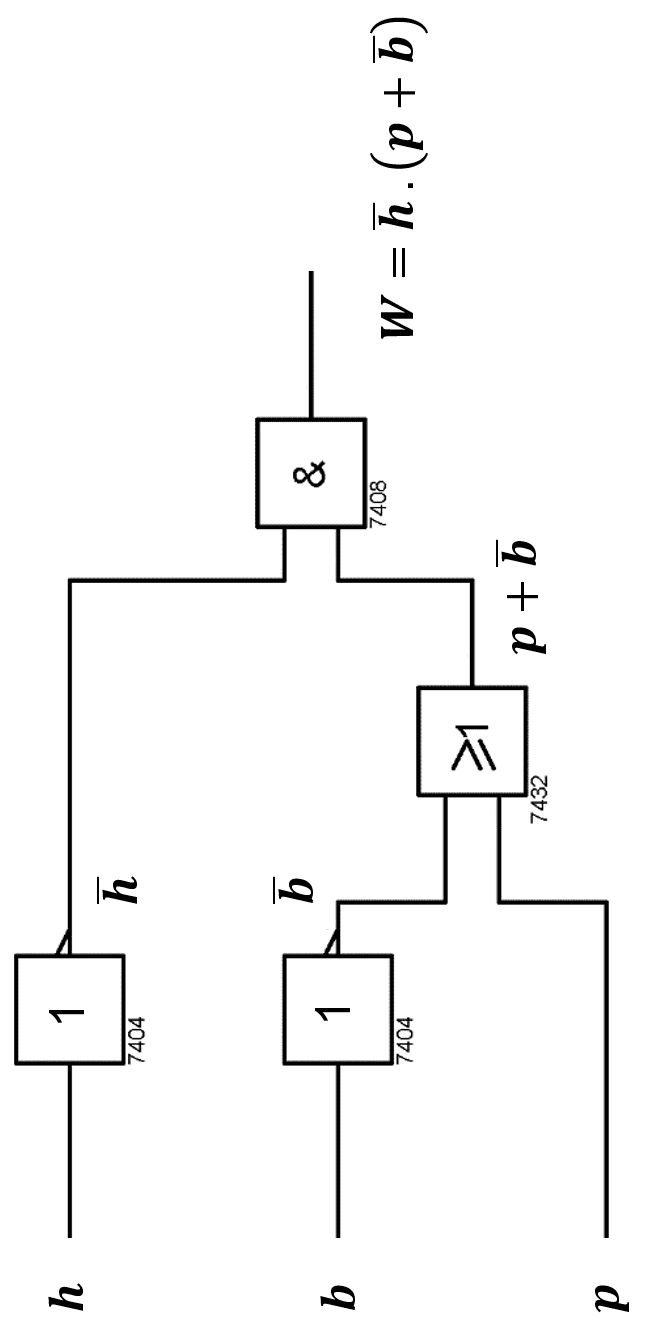
L’algèbre de Boole constitue l’ensemble de règles régissant le fonctionnement des systèmes logiques, en premier lieu desquels les systèmes combinatoires.
| ET logique | OU logique | |
| Élément neutre | a.1=a | a+0=a |
| Élément absorbant | a.0=0 | a+1=1 |
| Idempotence | a.a=a | a+a=a |
| Complémentation | a.¯a=0 | a+¯a=1 |
| Commutativité | a.b=b.a | a+b=b+a |
| Associativité | a.(b.c)=(a.b).c | a+(b+c)=(a+b)+c |
| Distributivité | a.(b+c)=a.b+a.c a+b.c=(a+b).(a+c) |
| Autres | ¯¯a=a a+a.b=a a+¯a.b=a+b |
Conception d’un circuit logique combinatoire :
- Lecture de la table de vérité issue des spécifications exprimées dans le cahier des charges.
- Extraction des expressions (équations logiques) des sorties depuis la table.
- Simplification des expressions des sorties (Algèbre de Boole ou tableaux de Karnaugh).
- Mise en place du logigramme à l’aide des portes logiques traduisant les fonctions logiques présentes dans les expressions des sorties.