Soit un solide S de masse m, de centre d’inertie G, en mouvement par rapport à un repère R(O,→x,→y,→z).
Soit M, un point du solide S.
L’énergie cinétique du solide S par rapport au repère R est définie par :
TS/R=12∫M∈S(→VM∈S/R)2dm
On pourrait montrer que l’énergie cinétique d’un solide S par rapport à R peut s’exprimer à partir des torseurs cinétique et cinématique :
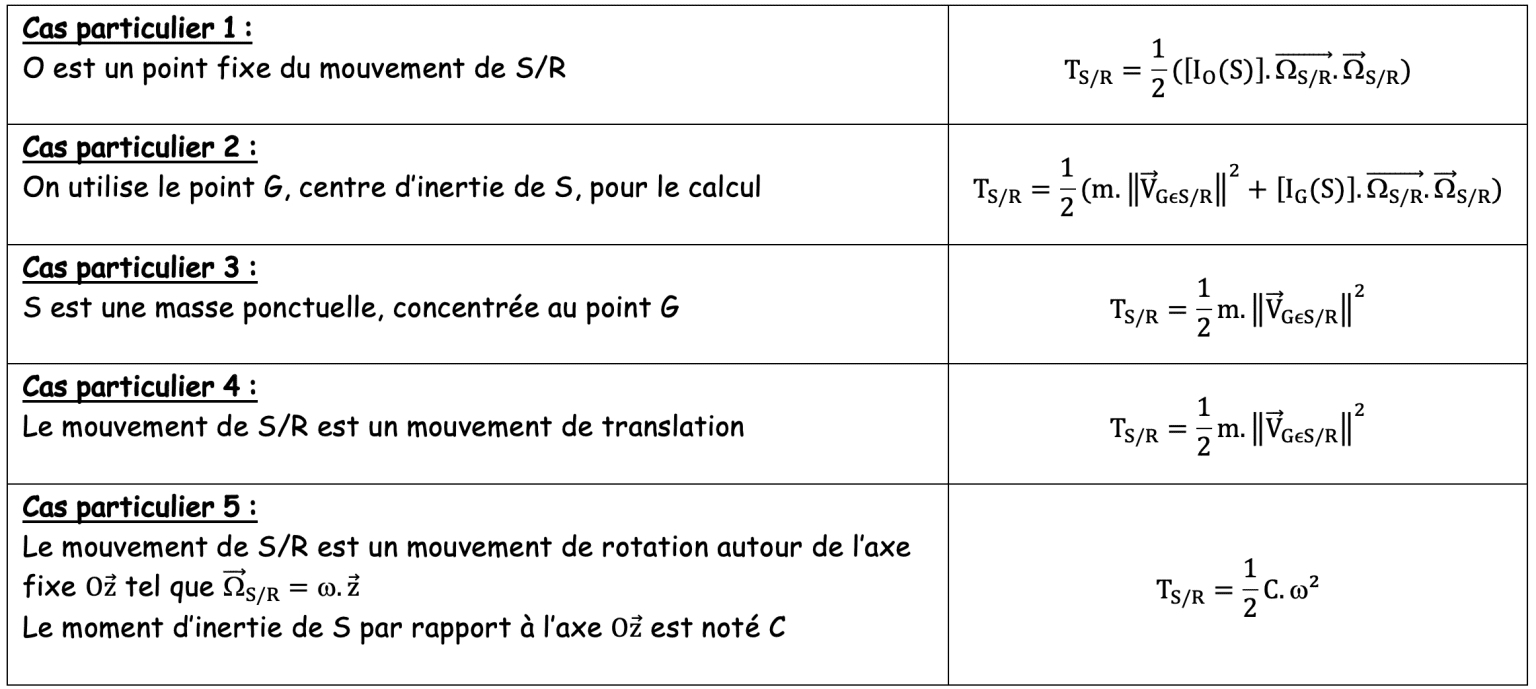
TS/R=12{CS/R}⊗{VS/R}
{VS/R}={→ΩS/R→VA∈S/R}A : torseur cinématique du solide S dans son mouvement par rapport à R.
{CS/R}={m⋅→VG∈S/R→σA(S/R)}A : torseur cinétique du solide S dans son mouvement par rapport à R
☠️
{VS/R} et {CS/R} doivent être exprimés au même point :
TS/R = 12{m⋅→VG∈S/R→ΓA(S/R)}A⊗{→ΩS/R→VA∈S/R}A
TS/R = 12(m⋅→VG∈S/R⋅→VA∈S/R+→σA(S/R)⋅→ΩS/R)
Si S=∑iSi alors TS/R=∑iTSi/R
Lorsqu’il existe des relations cinématiques entre les solides Si, il peut être intéressant d’exprimer l’énergie cinétique du système matériel S en fonction d’une seule variable cinématique.
On fait ainsi apparaître une « inertie équivalente ramenée sur un axe de rotation » ou une « masse équivalente ».



