Arithmétique

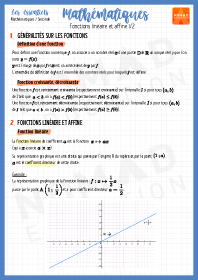
Divisibilité

Soit $a$ et $b$ deux entiers naturels non nuls.
S’il existe un nombre entier naturel $q$ tel que $a = b\times q$, on dit que :

• $a$ est un multiple de $b$ ;
• $a$ est divisible par $b$ ;
• $b$ est un diviseur de $a$.

Réciproquement, si $a$ et $b$ vérifient une des trois propriétés ci-dessus, alors il existe un nombre entier naturel $q$ tel que $a = b\times q$.

Exemple : 96 est divisible par 8 car $96 = 8\times 12$

Nombre premier

Un nombre premier est un nombre entier naturel (supérieur ou égal à $2$) qui admet exactement deux diviseurs : $1$ et lui-même.

Exemples : $2, 3, 5, 7, 11, 13$ sont des nombres premiers et il en existe une infinité.

• Un nombre entier est divisible par $2$ si son chiffre des unités est $0$ ; $2$ ; $4$ ; $6$ ou $8$.
• Un nombre entier est divisible par $3$ si la somme de ses chiffres est divisible par $3$.
• Un nombre entier est divisible par $5$ si son chiffre des unités est $0$ ou $5$.
• Un nombre entier est divisible par $9$ si la somme de ses chiffres est divisible par $9$.
• Un nombre entier est divisible par $10$ si son chiffre des unités est $0$.

Exemples :

• $465$ est divisible par $5$ car son chiffre des unités est $5 : 465 = 5\times 93$.
• $138$ est divisible par $3$ car $1 + 3 + 8 = 12$ est divisible par $3 : 138 = 3\times 46$.
• $522$ est divisible par $9$ car $5 + 2 + 2 = 9$ est divisible par $9 : 522 = 9\times 58$.