Émission et propagation d’un son
📝 Mini-cours GRATUIT
🍀 Fiches de révision PREMIUM

Chimie / La matière au niveau microscopique
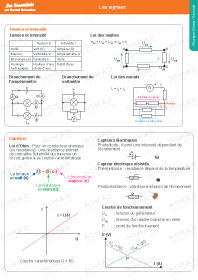
Physique / Les signaux

Chimie / Transformations

Physique / Les ondes

Chimie / La matière au niveau macroscopique

Physique / Mécanique



