Modéliser une action sur un système

Une action mécanique est capable de modifier le mouvement d’un objet ou de le déformer. Il existe des actions de contact (contact entre le système étudié et l’extérieur) et à distance. Une action mécanique est modélisée par une force ayant 4 caractéristiques : 

• sa direction (celle de la droite d’action de la force)
• son sens (celui de la force)
• son point d’application 
• sa valeur ou norme s’exprimant en Newton N

Chaque force est représentée par un vecteur force.

Principe des actions réciproques

Si deux corps $\rm A$ et $\rm B$ sont en interaction, alors la force exercée par le corps $\rm D_1$ sur le corps $\rm D_2$ a la même norme $\rm F_{A/B} = F_{B/A}$, la même direction et un sens opposé à celle exercée par le corps $\rm B$ sur le corps $\rm A$.
$\rm \vec F_{A/B} = - \vec F_{B/A}$

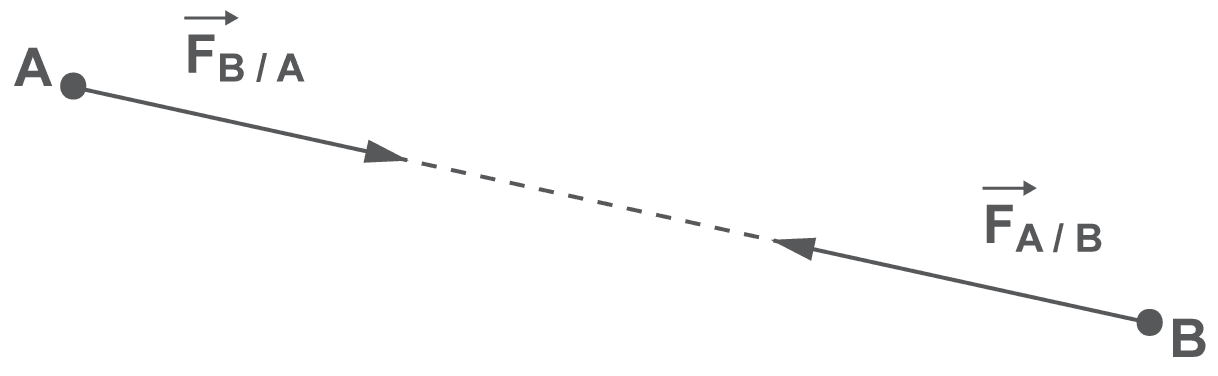
Exemple de forces :

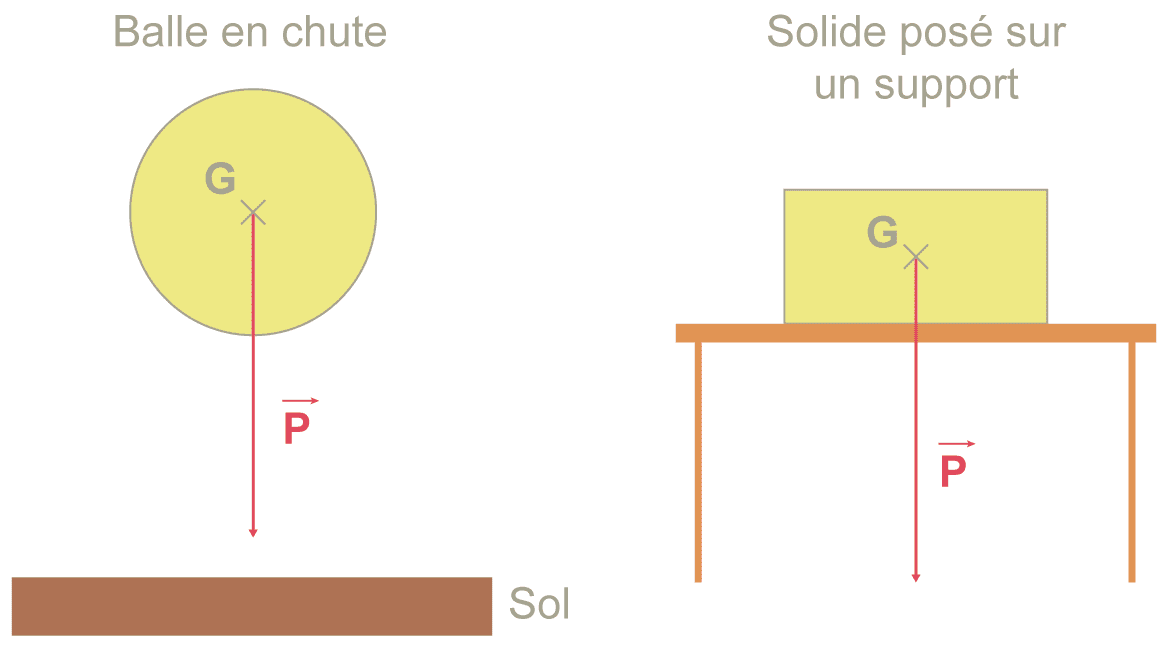
• Le poids noté $\rm P$ ayant pour caractéristique son point d’application (centre de gravité de l’objet) ; sa direction (verticale) ; son sens (de l’objet vers le centre de la Terre (vers le bas)) et sa norme $\rm P = m \times g$ avec $\rm P$ le poids en Newton N, $\rm m$ masse de l’objet en kg et $\rm g$ intensité de la pesanteur en $\rm N.kg^{-1}$.

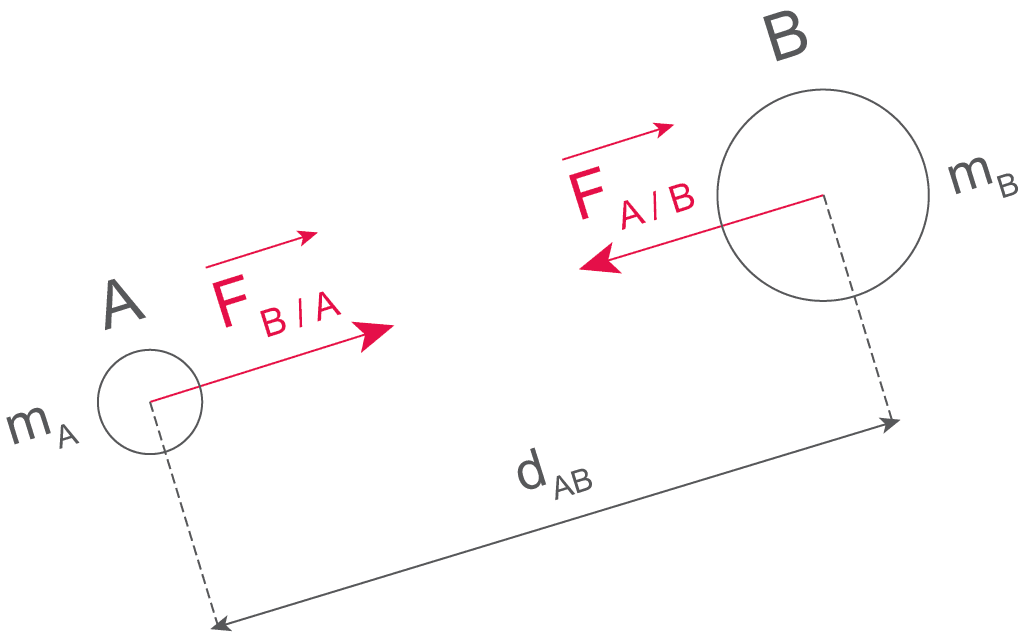
• l’interaction gravitationnelle : si un corps $\rm A$ et un corps $\rm B$ ponctuels possèdent respectivement une masse $\rm m_A$ et une masse $\rm m_B$ et sont séparés par une distance $\rm d$, alors la valeur $\rm F$ de la force de gravitation qui s’exerce entre eux est :
  $\displaystyle \rm F_{A/B} = F_{B/A} = G \times \frac{m_A \times m_B}{d^2}$
  Dans cette formule, on a : 
  les masses $\rm m_A$ et $\rm m_B$ exprimées en kg ;
  la distance $\rm d$ exprimée en m ;
  la constante de gravitation $\rm G$ égale à $\rm 6,67 \times 10^{-11}~m^2.kg^{-2}$.