Résoudre des problèmes de géométrie
📝 Mini-cours GRATUIT
Propriétés des quadrilatères
📄 Exercices pas à pas PREMIUM

Démontrer des propriétés sur les triangles

Démontrer des propriétés sur les quadrilatères
📄 Prépare ton éval PREMIUM

Résoudre des problèmes de géométrie
🍀 Fiches de révision PREMIUM

Statistiques et probabilités

Fonctions carré, inverse, cube et racine carrée
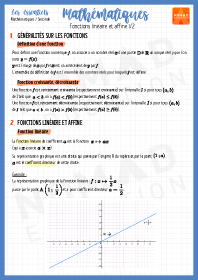
Fonctions linéaire et affine

Ensembles de nombres et arithmétique

Calcul littéral

Géométrie



