Aspects énergétiques dans un champ uniforme
📝 Mini-cours GRATUIT
📄 Annales PREMIUM

Annales corrigées Polynésie 2021 – Physique-Chimie

Annales corrigées de Métropole 2022 – Spé Physique-chimie sujet 2

Annales corrigées Amérique du Nord 2021 — Physique-Chimie Amérique du Nord

Annales corrigées de Métropole 2022 – Spé Physique-chimie sujet 1
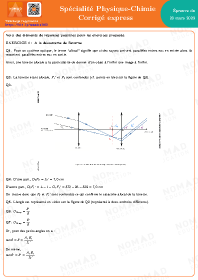
Annales corrigées Métropole 2023 — Spé Physique-Chimie sujet 1

Annales corrigées Métropole 2023 — Spé Physique-Chimie sujet 2
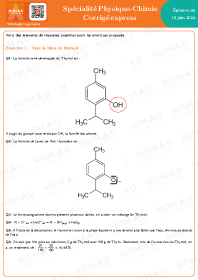
Annales corrigées Métropole 2024 — Spé Physique-Chimie sujet 1

Annales corrigées Métropole 2024 — Spé Physique-Chimie sujet 2



