Description d’un mouvement

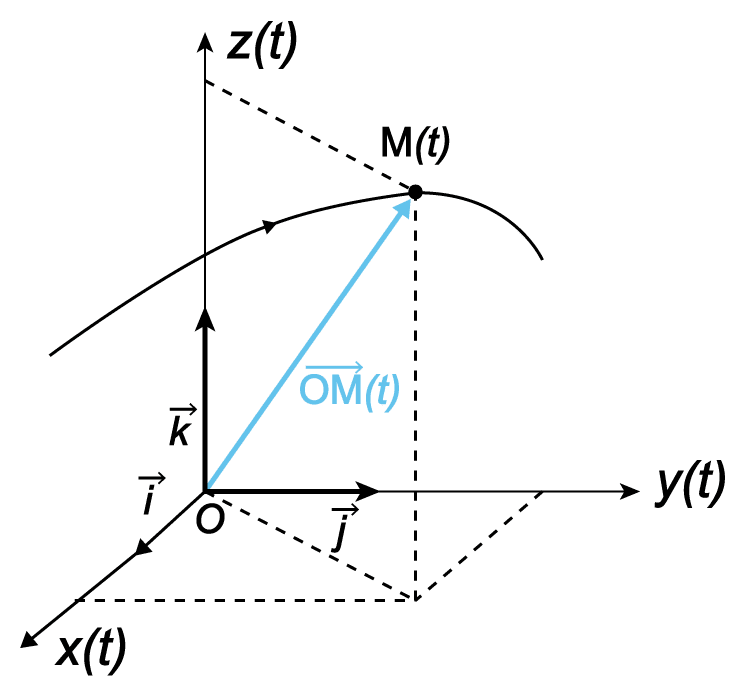
Le référentiel est un endroit de référence par rapport auquel on étudie le mouvement d’un mobile.

À chaque référentiel est associé :

• un repère d’espace pour quantifier la position ;
• un repère de temps (une horloge) pour associer une date à chaque position.

La position d’un mobile $\rm M$ dans un repère $(\mathrm O, \vec i, \vec j, \vec k)$ est donné par son vecteur-position $\rm \overrightarrow{OM}$ :

$\overrightarrow{\rm OM} (t)=\begin{pmatrix}x(t)\\y(t)\\z(t)\end{pmatrix}$ $\Leftrightarrow$ $\overrightarrow{\rm OM}(t) = x(t) \vec i + y(t) \vec j + z(t) \vec k$

L’ensemble des points, occupé successivement par le mobile $\rm M$ au cours du temps, est appelé trajectoire.

Le vecteur vitesse

Le vecteur vitesse $\vec v(t)$ caractérise la variation du vecteur position en fonction du temps. Il s'exprime donc comme la dérivée par rapport au temps de son vecteur position.

Le vecteur vitesse instantanée au point $\mathrm M$ s'écrit donc :

$\boxed{\overrightarrow{v(t)} = \frac{\rm d\overrightarrow{OM}}{\mathrm dt}} \left\{\begin{array}{ll}t \text{ en s}\\ \rm OM \text{ en m}\\ v \text{ en } \rm m.s^{-1}\end{array}\right.$

$\vec v(t) = v_x(t) \vec i + v_y (t) \vec j + v_z(t)\vec k$ avec $\vec v \left|\begin{array}{lll}v_x = \dfrac{\mathrm dx}{\mathrm dt}\\v_y = \dfrac{\mathrm dy}{\mathrm dt}\\v_z = \dfrac{\mathrm dz}{\mathrm dt}\end{array}\right.$

Les caractéristiques du vecteur vitesse sont les suivantes :

$\vec v(t)\left\{\begin{array}{lll}\scriptstyle \text{direction : tangent à la trajectoire}\\ \scriptstyle\text{sens : celui du mouvement}\\ \scriptstyle\text{valeur (norme) : } \|\vec v\| = v = \sqrt{v_x^2+v_y^2+v_z^2}\end{array}\right.$

Le vecteur accélération

Le vecteur accélération $\vec a (t)$ caractérise la variation du vecteur vitesse en fonction du temps. Il s'exprime donc comme la dérivée par rapport au temps de son vecteur vitesse.

Le vecteur accélération au point $\mathrm M$ s'écrit donc :

$\boxed{\overrightarrow{a(t)} = \frac{\mathrm d\vec v}{\mathrm dt} = \frac{\rm d^2\overrightarrow{OM}}{\mathrm dt^2}} \left\{\begin{array}{ll}t \text{ en s}\\ v \text{ en } \rm m.s^{-1}\\ a \text{ en } \rm m.s^{-2}\end{array}\right.$

$\vec a(t) = a_x(t) \vec i + a_y (t) \vec j + a_z(t)\vec k$ avec $\vec a \left|\begin{array}{lll}a_x = \dfrac{\mathrm dv_x}{\mathrm dt} = \dfrac{\mathrm d^2x}{\mathrm dt^2}\\a_y = \dfrac{\mathrm dv_y}{\mathrm dt} = \dfrac{\mathrm d^2y}{\mathrm dt^2}\\a_z = \dfrac{\mathrm dv_z}{\mathrm dt} = \dfrac{\mathrm d^2z}{\mathrm dt^2}\end{array}\right.$

Les caractéristiques du vecteur accélération sont les suivantes :

$\vec a(t)\left\{\begin{array}{lll}\scriptstyle \text{direction : celle du vecteur } \overrightarrow{\Delta v}(t)\\ \scriptstyle\text{sens : celui du vecteur } \overrightarrow{\Delta v}(t)\\ \scriptstyle\text{valeur (norme) : } a = \frac{\Delta v}{\Delta t} = \|\vec a\| = \sqrt{a_x^2+a_y^2+a_z^2}\end{array}\right.$

Des exemples de mouvements

Mouvements rectilignes

Repère de Frenet

$\vec a = a_{\rm T}\overrightarrow{u_{\rm T}} + a_{\rm N}\overrightarrow{u_{\rm N}}$ avec $\boxed{a_{\rm T} = \dfrac{\mathrm dv}{\mathrm dt}}$ et $\boxed{a_{\rm N} = \left(\dfrac{v^2}{\rm R}\right)}$

Mouvements circulaires

Deuxième loi de Newton

Dans un référentiel Galiléen $\boxed{\displaystyle \sum \mathrm{\vec F_{ext}} = \mathrm m\dfrac{\mathrm d\vec v}{\mathrm dt}= \mathrm m\vec a}$

Rappel : $\rm 1^{ère}$ loi de Newton

« Tout corps persévère dans son état de repos ou de mouvement rectiligne uniforme si les forces qui s’exercent sur lui se compensent ».

$\displaystyle\bf \sum \vec F_{ext} = \vec 0$