Graphes

Vocabulaire :

Un graphe est composé d'un certain nombre de sommets et d'arêtes reliant entre eux certains sommets.

Le degré d'un sommet est le nombre d'arêtes partant de ce sommet.

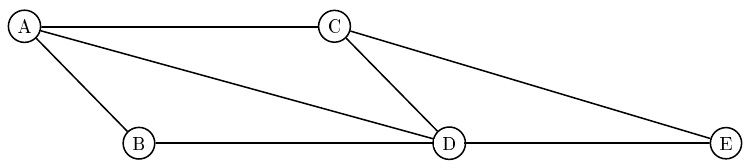
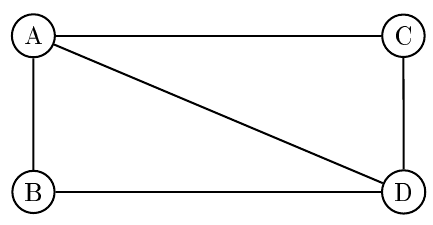
Sur notre exemple, les sommets sont A, B, C, D et E. Une arête relie A et B, mais aucune arête ne relie B et C. B et E sont de degré 2, A et C sont de degré 3, D est de degré 4.

L'ordre d'un graphe est le nombre de sommets, ici 5.

Un graphe complet est un graphe où tous les sommets sont reliés 2 à 2 par des arêtes. Ce n'est pas le cas ici, car B et C ne sont pas directement reliés par une arête (ni E et A, etc...).

Une chaîne est un ensemble d'arêtes qui se suivent, autrement dit un chemin que l'on peut parcourir dans le graphe, par exemple ici A-D-C-E.

Un cycle est une chaîne dont les premier et dernier sommets sont les mêmes, par exemple ici A-D-C-A.   

Un graphe est connexe si deux sommets quelconques peuvent être reliés par une chaîne. Le graphe représenté est donc connexe (mais pas complet).

Propriétés :

Une chaîne eulérienne est une chaîne qui passe une et une seule fois par chaque arête du graphe.

Théorème : un graphe admet une chaîne eulérienne si et seulement si ce graphe possède exactement 2 sommets de degré impair. Toute chaîne eulérienne démarre et finit, dans ce cas, par ces 2 sommets. 

Dans notre exemple, A et C sont les seuls sommets de degré impair, il existe donc des chaînes eulériennes: A-B-D-E-C-D-A-C en est une. 

Astuce : faites le tour du graphe à l'extérieur, puis faites l'intérieur. En général, ça marche.

Un cycle eulérien est un cycle qui passe une et une seule fois par chaque arête du graphe.

Théorème : un graphe admet un cycle eulérien si et seulement si ce graphe ne possède aucun sommet de degré impair.

Dans notre exemple, le graphe n'admet pas de cycle eulérien. 

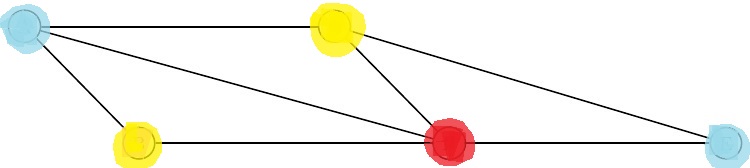
Le nombre chromatique d'un graphe est le nombre minimum de couleurs à utiliser pour colorier tous les sommets en respectant la règle suivante: 2 sommets reliés par une arête ne doivent pas avoir la même couleur.

Théorème : on a l'encadrement ${ o\leq \gamma \leq d+1 } $, où ${ o } $ désigne l'ordre d'un sous-graphe complet contenu dans le graphe, ${\gamma }$ désigne le nombre chromatique, et ${ d }$ est le degré maximum du graphe. 

Dans notre exemple, cela donne ${ 3\leq \gamma\leq 5} $, et en fait ${\gamma }$ = 3 :

Si G est un graphe pondéré, l'algorithme de Dijkstra permet de trouver le plus court chemin reliant 2 sommets du graphe.

Par exemple, voici un graphe :

L'objectif est de trouver le plus court chemin allant de G à D.

Pour répondre à la question, on part de G, on regarde quels sont les sommets accessibles à partir de là, et on progresse de proche en proche. On note les résultats, qui ne sont pas définitifs, soit au brouillon sur le graphe, soit dans un tableau :

Pour conclure, on lit le tableau à l'envers : arrivé en D, le plus court chemin vient de F (longueur totale 165), qui lui-même vient de B (longueur 130 de G à F), qui lui-même vient de C (longueur 95 de G à B),...

Ici, le plus court chemin de G à D est donc G-H-C-B-F-D.

La matrice d'adjacence d'un graphe indique quels sommets sont reliés par des arêtes.

Prenons l'exemple de ce graphe :

Pour créer la matrice, il suffit de se souvenir que ligne i, colonne j, on met 1 s'il y a une arête qui relie le sommet i au sommet j et 0 sinon. On peut pour aider, mettre les noms des sommets en ligne et en colonne, comme ceci :

A n'est pas relié à lui-même mais à B,C et D par des arêtes, donc on met 0,1,1,1 dans la première ligne, et ainsi de suite...
Lorsque le graphe n'est pas orienté, la matrice obtenue est symétrique.
Pour un graphe orienté, le principe est exactement le même sauf que la matrice n'est plus symétrique :

Propriété : Si ${M}$ est la matrice d'adjacence d'un graphe orienté ou non, le nombre situé ligne i colonne j dans la matrice ${M^n}$ est le nombre de chemins de longueur ${n }$ reliant le sommet i au sommet j.

Un graphe probabiliste (ou probabilisé) est un graphe orienté et pondéré vérifiant :

• Tous les poids appartiennent à l’intervalle [0;1].
• Il y a au plus une arête entre deux sommets quelconques du graphe.
• La somme des poids des arêtes issues d’un sommet est égale à 1.

Remarque : On dit aussi qu’un graphe probabilisé à $n$ sommets est associé à une chaîne de Markov à $n$ états.

Si G est un graphe probabiliste, comme celui-ci :

on peut lui associer une matrice de transition, ${M}$, dans laquelle on met ligne ${i}$, colonne ${j}$, la probabilité d'aller du ${i^e}$ au ${j^e}$ sommet, ce qui donne ici :

Si ${P_0}$ est l'état initial, on a alors les formules :

${P_{n+1}=P_n\times M}$

et

${P_{n}=P_0\times M^n}$

Enfin, pour trouver l'état stable de la matrice, il faut résoudre le système :

${P=P\times M}$

Sans oublier que la somme des probabilités vaut ${1}$. Autrement dit, si

${P=(x,y)}$ cela donne :

${\left\{\begin{matrix}
0.6x + 0.8y=x \\0.4x+0.2y=y\\x+y=1
\end{matrix}\right. }$

Qui est équivalent à :

$ {\left\{\begin{matrix}
-0.4x + 0.8y=0 \\x+y=1
\end{matrix}\right.}$