Mouvement dans un champ de gravitation

Les lois de Kepler

Première loi

Dans le référentiel héliocentrique, le centre de chaque planète décrit une trajectoire elliptique dont le Soleil S est l'un des foyers.

Deuxième loi

Le rayon SM qui relie la planète M au Soleil S balaie des aires égales en des temps égaux.

Troisième loi

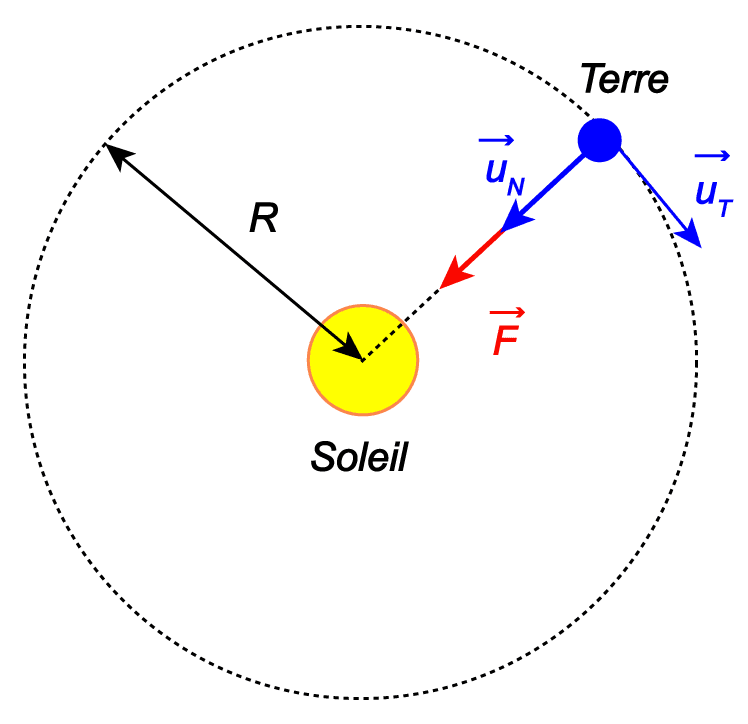
Mouvement circulaire uniforme de la Terre autour du Soleil

Définition du système d'étude

Système : Terre de masse $\rm M_T$

Référentiel : héliocentrique supposé galiléen

Bilan des forces

Application de la deuxième loi de Newton

Deuxième Loi de Newton : $\rm \sum \overrightarrow F = \overrightarrow F = M_T \cdot \mathcal{\overrightarrow a}$

$\rm \overrightarrow F = M_T \cdot \mathcal{\overrightarrow a} \Leftrightarrow \dfrac{G.M_TM_S}{R^2}\overrightarrow{\mathcal u_N}$ $\rm = M_T(\mathcal a_T\overrightarrow{\mathcal u_T} + \mathcal a_N\overrightarrow{\mathcal u_N})$ $\rm \Leftrightarrow \dfrac{G.M_T.M_S}{R^2}\overrightarrow{\mathcal u_N}$ $= \rm M_T\mathcal a_T\overrightarrow{\mathcal u_T} + M_T\mathcal a_N\overrightarrow{\mathcal u_N}$

Identification des composantes

Donc, par identification : $\left\{\begin{array}{lll}\rm M_T.\mathcal a_N = \dfrac{G.M_T.M_S}{R^2}\\ \rm \mathcal a_T = 0\end{array}\right.$ $\Leftrightarrow$ $\left\{\begin{array}{ll}a_{\rm N} \rm = \dfrac{G.M_S}{R^2}\\a_{\rm T} = 0\end{array}\right.$

Conséquences du mouvement

Or si $a_T = 0$ alors $\dfrac{\mathrm dv}{\mathrm dt} = 0$ car par définition $a_T = \dfrac{\mathrm dv}{\mathrm dt}$.

Comme $\dfrac{\mathrm dv}{\mathrm dt} = 0$ alors la norme de la vitesse est constante.

Ainsi, si la trajectoire d'un objet en orbite gravitationnelle est circulaire alors son mouvement est uniforme.

Expression de la vitesse orbitale

Comme $a_{\rm N} = \dfrac{v^2}{\rm R}$, on a donc $\dfrac{v^2}{\rm R} = \rm \dfrac{G.M_S}{R^2}$ $\Leftrightarrow$

Période de révolution

La période de révolution $\rm T$ est le temps nécessaire à l'objet (ici la Terre) pour faire un tour sur son orbite. La longueur $\rm L$ d'une orbite est égale au périmètre du cercle, soit : $\rm L = 2 \pi R$

Donc $v = \dfrac{\rm L}{\Delta t} = \rm \dfrac{2\pi R}{T}$ donc $\rm T = 2\pi \sqrt{\dfrac{R^3}{GM_S}}$ en utilisant l'expression de $v$ trouvée précédemment.