Mouvement dans un champ de pesanteur uniforme

Les lois de Newton

1re loi de Newton : Principe d’inertie.

Tout corps persévère dans son état de repos ou de mouvement rectiligne uniforme si les forces qui s’exercent sur lui se compensent (l’« état » du corps dépend des conditions initiales).

2e loi de Newton = Principe fondamental de la dynamique 

$\boxed{\displaystyle \rm \sum \overrightarrow{F_{ext}} = m\vec{\mathcal a}}$

3e loi de Newton : Principe d’action réaction

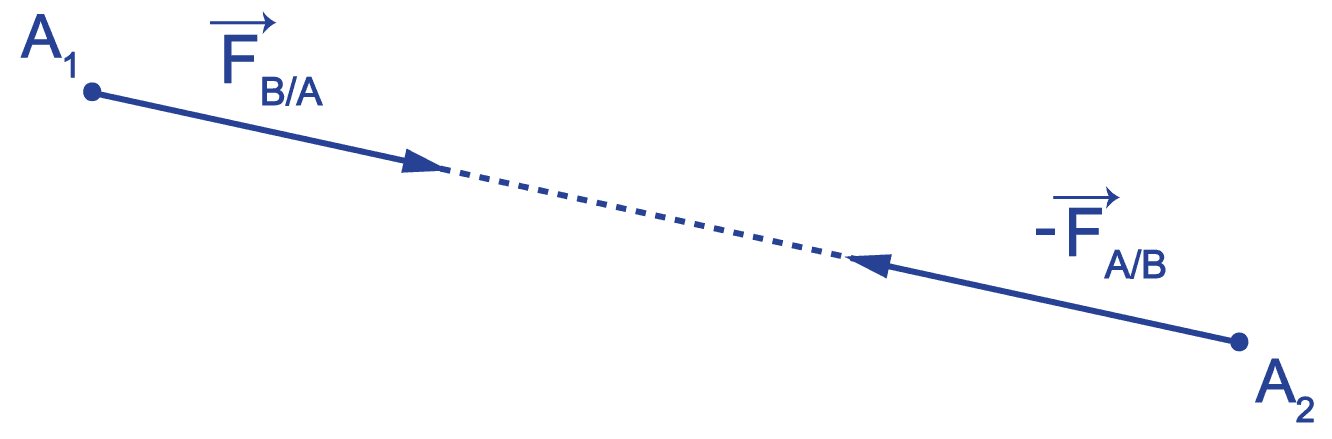
Si un corps $\rm A$ exerce sur un corps $\rm B$ une force $\rm \overrightarrow{F}_{A/B}$, alors $\rm B$ exerce sur $\rm A$ une force $\rm \overrightarrow{F}_{B/A}$ telle que : $\rm \overrightarrow{F}_{A/B} = \overrightarrow{-F}_{B/A}$.

Que les actions mécaniques entre $\bf A$ et $\bf B$ soient de contact ou à distance, que ces corps soient en mouvement ou immobiles, ces deux forces ont la même direction d'’action : la droite $\rm (AB)$ ; la même intensité $\rm (F_{A/B} = F_{B/A})$ mais des sens opposés.

Mouvement dans un champ de pesanteur uniforme

Système : balle de masse $\rm m$
Référentiel : terrestre supposé galiléen
Bilan des forces : poids de la balle

2e loi de Newton :

• $\displaystyle \rm \sum \overrightarrow{F_{ext}} = m\cdot \overrightarrow{\mathcal{a(t)}}$
• $\rm \vec P = m\cdot \overrightarrow{\mathcal{a(t)}}$
• $\mathrm m \cdot \vec g = \mathrm m\cdot \overrightarrow{a(t)}$
• $\overrightarrow{a(t)} = \vec g = \overrightarrow{\rm cte}$

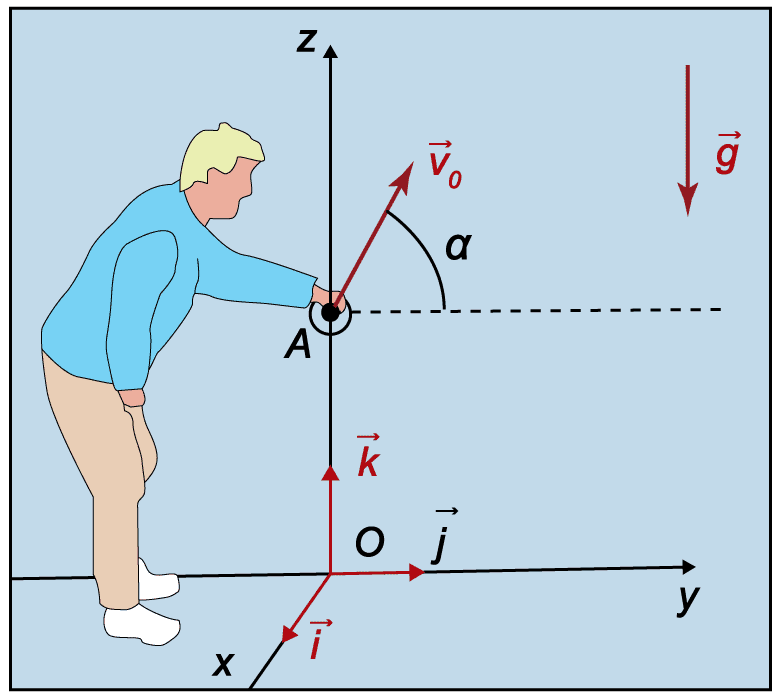
On projette sur les 3 axes.

Grâce à ces deux équations, on peut obtenir l’équation de la trajectoire : $(1)$ Nous donne $t = \dfrac{y}{v_0\times \cos \alpha}$.

On remplace dans $(2)$ : $\boxed{ z(y) = -1/2 \times g \times \frac{y^2}{v_0^2 \times \cos^2 \alpha} + \tan \alpha \times y + \rm OA}$