📝 Mini-cours GRATUIT

Je m’inscris pour accéder gratuitement à ce contenu

Transformations nucléaires

Désintégration radioactive

Un noyau instable (appelé noyau père) se désintègre spontanément en se transformant en un noyau d’un autre élément chimique (appelé noyau fils) en émettant une particule et éventuellement un rayonnement gamma.

Particule émise	Symbole	Radioactivité
Électron	$\color{limegreen}{\rm _{-1}^0e}$	$\color{black}{\beta^-}$	$\color{black}{\scriptstyle \rm ^A_Z X \rightarrow ^A_{Z+1} Y + ^0_{-1}e}$
Positron	$\color{limegreen}{\rm _1^0e}$	$\color{black}{\beta^+}$	$\color{black}{\scriptstyle \rm ^A_Z X \rightarrow ^A_{Z-1} Y + ^0_{1}e}$
Noyau d’hélium 4	$\color{limegreen}{\rm _2^4He}$	$\color{black}{\alpha}$	$\color{black}{\scriptstyle \rm ^A_Z X \rightarrow ^{A-4}_{Z-2} Y + ^4_2He}$

$\rm (N,Z)$ permet d’identifier le type de radioactivité et le noyau fils émis.

Équation de désintégration

Au cours d’une transformation nucléaire il y a conservation du :

Nombre de charge $\rm Z$
Nombre de masse $\rm A$

Exemple :

$\rm ^{210}_{84}Po \rightarrow ^{206}_{82} Pb + ^4_2 He$

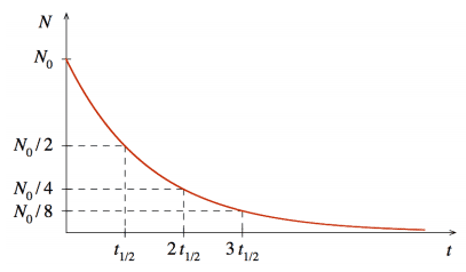
Loi de décroissance radioactive

Le nombre $\rm N(t)$ de noyaux radioactifs contenus dans un échantillon varie selon la loi.

$\boxed{\rm N(t) = N_0\cdot e^{-\lambda \cdot t}}$

Avec $\rm N_0$ nombre initial de noyaux radioactifs et λ constante radioactive en $\rm s^{-1}$ si $\rm t$ est en $\rm s$ .

La demi-vie d’un noyau radioactif est égale à la durée au bout de laquelle la moitié des noyaux radioactifs initialement présents se sont désintégrés :

$\boxed{\displaystyle \rm t_{1/2} = \frac{\ln 2}{\lambda}}$

L’Activité $\rm A$ d’un échantillon radioactif est le nombre moyen de désintégration s’y produisant par seconde. Elle s’exprime en becquerel, noté $\rm Bq$ .