Arbre
Dans un arbre, les données sont organisées de manière à former une arborescence. Il est souvent nécessaire de :
- calculer la taille de l’arbre ;
- calculer la hauteur de l’arbre ;
- effectuer une opération de recherche ou de traitement sur les données de l’arbre.
Pour effectuer ces opérations, il faut être en mesure de parcourir l’arbre : cela permettra de compter le nombre de nœuds (pour connaître la taille de l’arbre), la profondeur maximale (pour connaître sa hauteur) ou d’analyser/traiter les nœuds. Un arbre peut être parcouru en largeur ou en profondeur.
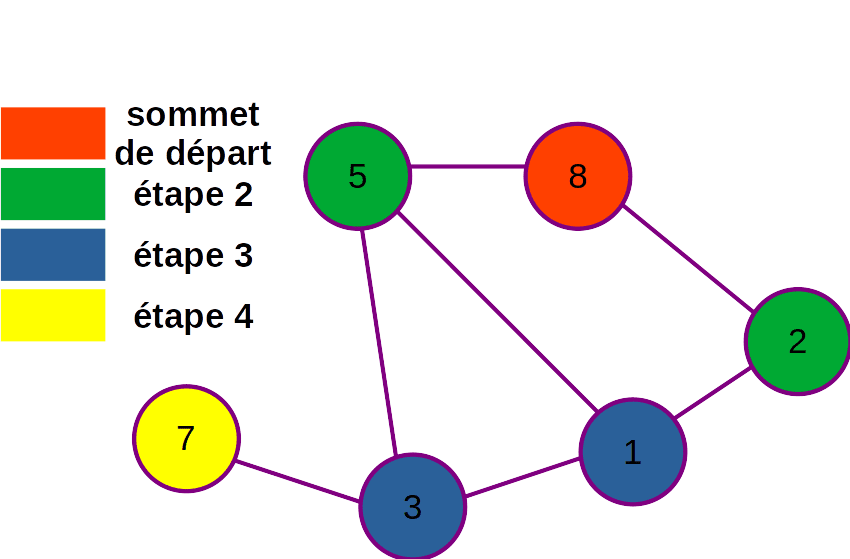
Parcours en largeur
On commence par parcourir tous les nœuds de niveau 0, puis tous ceux de niveau 1, etc.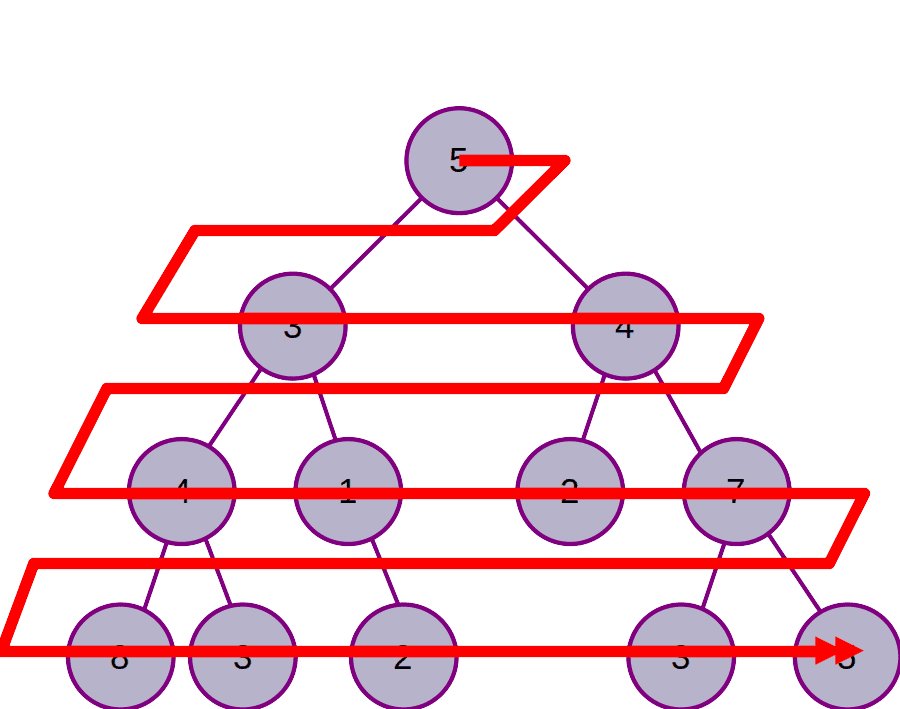
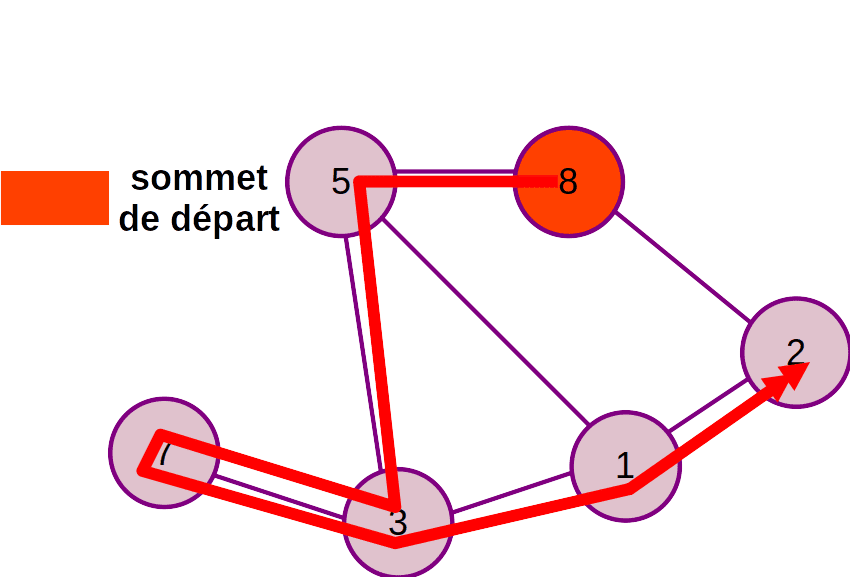
Parcours en profondeur
On descend le plus en profondeur possible, en explorant les arêtes de gauche de l’arbre. Une fois arrivé sur une feuille, on remonte jusqu’à tomber sur un nœud possédant une arête droite, qu’on va explorer, et ainsi de suite.
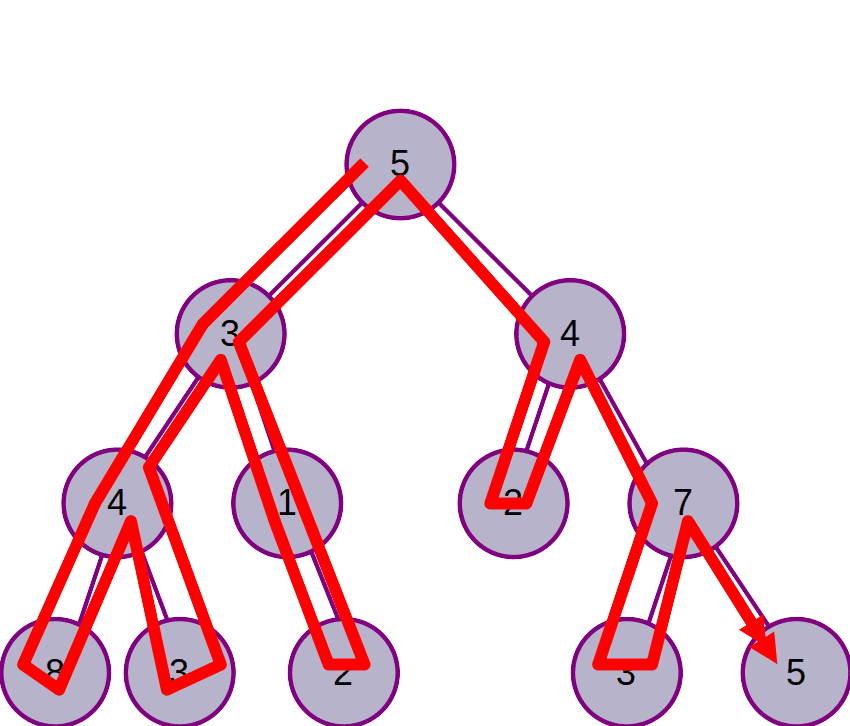
Dans un parcours en profondeur, les nœuds seront traversés plusieurs fois pendant le parcours. On peut décider d’analyser/traiter les données d’un nœud :
- lors de l’arrivée sur le nœud, en descendant l’arbre : on parle alors de parcours préfixe ;
- entre la fin de l’exploration de l’arête gauche du nœud (y compris si elle est vide) et le début de l’exploration de l’arête droite du nœud : on parle alors de parcours infixe ;
- lorsque l’on quitte le nœud, pour remonter dans l’arbre : on parle alors de parcours postfixe.