L’énergie mécanique, notée $\rm E_m$, d'un corps est la somme de son énergie cinétique $\rm E_c$ et son énergie potentielle de pesanteur $\rm E_{pp}$ :
$\rm E_m = E_c + E_{pp}$
Conservation de l’énergie mécanique
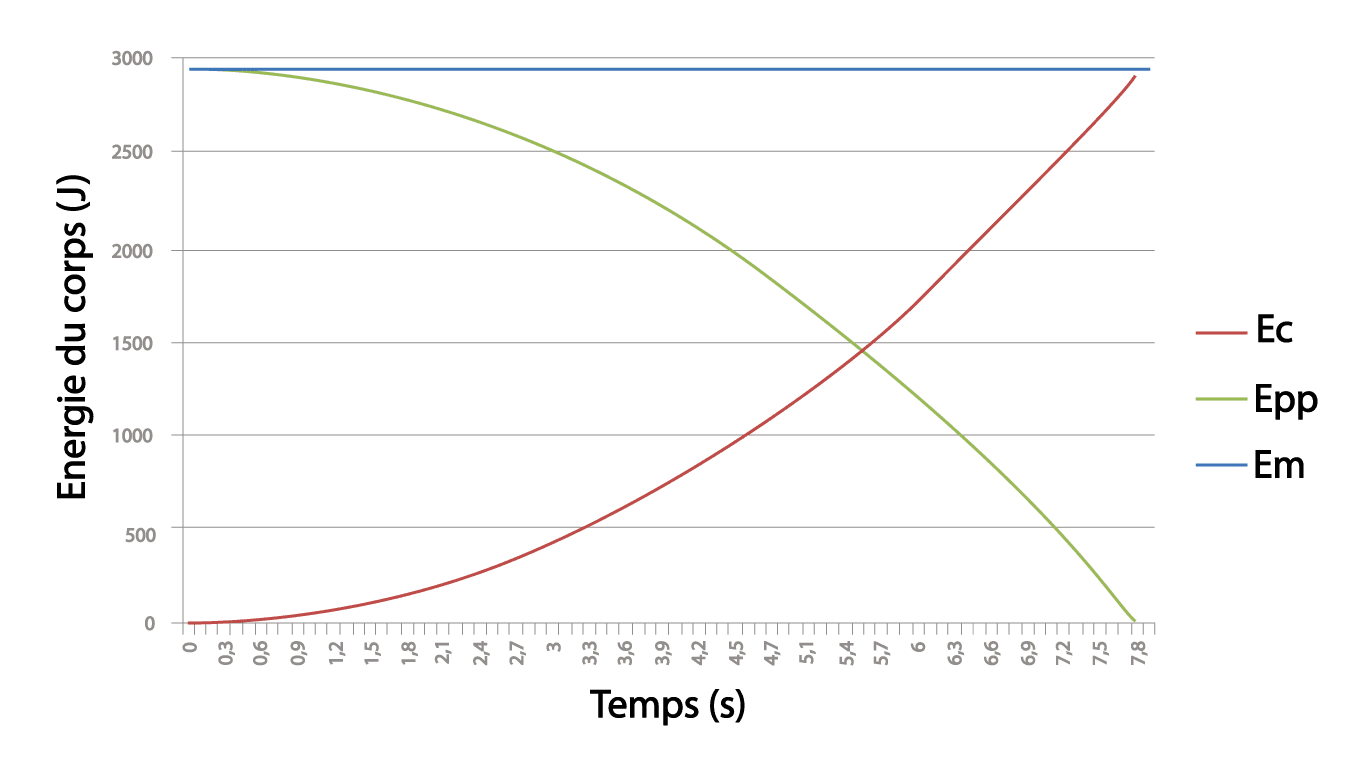
Au cours d’une chute sans frottements, l’énergie mécanique est constante : on dit qu’elle se conserve. La diminution de l’énergie potentielle de pesanteur est compensée par l’augmentation de l’énergie cinétique.
La variation d’énergie cinétique $\rm E_c$ d'un solide entre $\rm A$ et $\rm B$ est liée au travail des forces appliquées entre $\rm A$ et $\rm B$ : c’est le théorème de l’énergie cinétique :
$\displaystyle\bf E_{c_B} - E_{c_A} = \sum W_{AB}(\vec F)$
$\dfrac{1}{2}.\mathrm m.v_{\rm B}^2 - \dfrac{1}{2}.\mathrm m.v_{\rm A}^2 = \rm\Delta E_c = \sum W_{AB}(\vec F)$ avec $\rm A$ le point de départ et $\rm B$ le point d’arrivée.
Dans le cas d’un condensateur plan