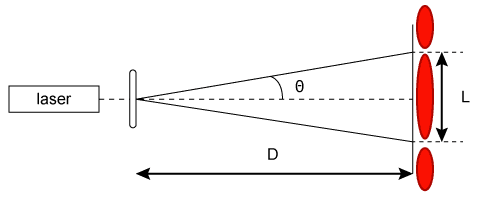
En mécanique ondulatoire, on parle d'interférences lorsque deux ondes de même type se rencontrent et interagissent l'une avec l'autre. En pratique, ce phénomène est observable si les ondes progressives périodiques produites par deux sources sont monochromatiques et de même longueur d’onde, ainsi que synchrones (ou dites cohérentes), ce qui est le cas lorsqu’une source initiale est dédoublée par un moyen quelconque (double fente par exemple).
Interférences constructives et destructives
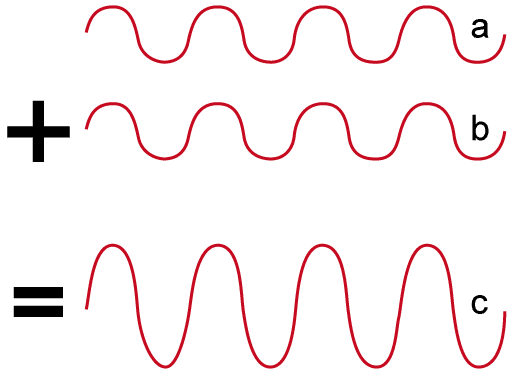
Si les creux et crêtes de deux ondes coïncident en un point, les ondes se renforcent : elles sont en phase et on parle d’interférences constructives.
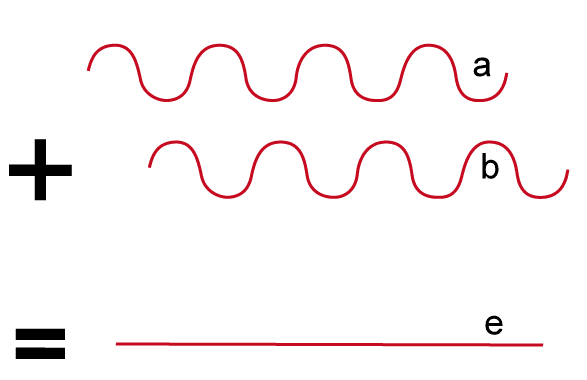
Si un creux de l’une coïncide avec une crête de l’autre, les ondes s’annulent : elles sont en opposition de phase et on parle d’interférences destructives.
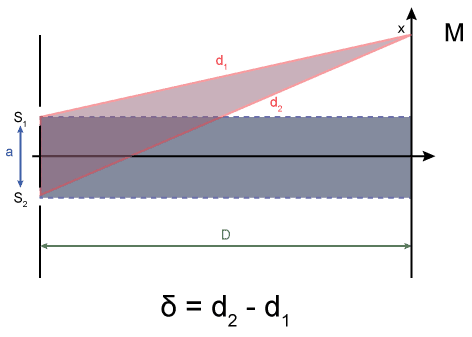
Différence de marche
La différence de marche en un point $\rm M$ est la différence entre les deux distances $\rm d_1$ et $\rm d_2$ parcourues par les ondes de longueur d’onde $\lambda$ à partir de $\rm S_1$ et $\rm S_2$.
Si $\rm \delta = k\cdot\lambda$, alors on obtient des interférences constructives. ($\rm k$ entier relatif).
Si $\rm \delta = \left(k + \dfrac{1}{2}\right)\cdot \lambda$, alors les interférences sont destructives.
Interfrange

La distance qui sépare les milieux de deux franges consécutives de même nature est appelée interfrange $\color{red}{i}$.
$i = \dfrac{\lambda\cdot \rm D}{a}$ :
- $\lambda$ = longueur d'onde dans le milieu $\rm (m)$
- $\rm D$ = distance entre les fentes de l'écran $\rm (m)$
- $a$ = écartement des centres des fentes $\rm (m)$
- $i$ = interfrange $\rm (m)$