Fonctions cosinus et sinus

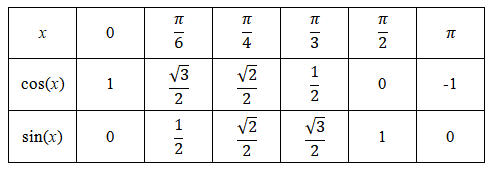
Valeurs remarquables

Cosinus et sinus d'angles associés

Formules pour le cosinus

Pour tout nombre réel $x$ :

• $\cos(-x) = \cos(x)$ (fonction paire)
• $\displaystyle \cos(x + \frac{\pi}{2}) = -\sin(x)$
• $\cos(x + \pi) = -\cos(x)$
• $\displaystyle \cos\left(x - \frac{\pi}{2}\right) = \sin(x)$

Formules pour le sinus

Pour tout nombre réel $x$ :

• $\sin(-x) = -\sin(x)$ (fonction impaire)
• $\displaystyle \sin\left(x + \frac{\pi}{2}\right) = \cos(x)$
• $\sin(x + \pi) = -\sin(x)$
• $\displaystyle \sin\left(x - \frac{\pi}{2}\right) = -\cos(x)$

Équation $\cos (x) = \cos(a)$

L'équation $\cos(x) = \cos(a)$ a pour solutions :

Fonction cosinus

La fonction cosinus est définie et dérivable sur $\mathbb{R}$. Pour tout $x\in \mathbb{R}$, $\cos'(x) = -\sin(x)$.

Elle est périodique de période $2\pi$ et sa représentation graphique (en bleu) est une sinusoïde de période $2\pi$.

La fonction cosinus est paire donc sa représentation graphique est symétrique par rapport à l'axe des ordonnées.

Fonction sinus

La fonction sinus est définie et dérivable sur $\mathbb{R}$. Pour tout $x\in \mathbb{R}$, $\sin'(x) = \cos(x)$.

Elle est périodique de période $2\pi$ et sa représentation graphique (en noir) est une sinusoïde de période $2\pi$.

La fonction sinus est impaire donc sa représentation graphique est symétrique par rapport à l'origine du repère.