Optimisation du transport de l’électricité
📝 Mini-cours GRATUIT
Optimiser le réseau de distribution
🍀 Fiches de révision PREMIUM
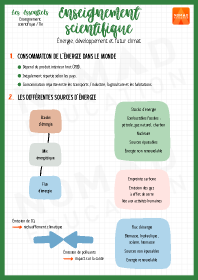
Énergie, développement et futur climat

L’évolution comme grille de lecture du monde
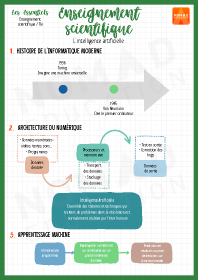
L’intelligence artificielle

Énergie, développement et futur climat

L’évolution comme grille de lecture du monde

L’intelligence artificielle



