Définition et variation
La fonction inverse () est définie et dérivable sur les intervalles et , et sa dérivée est la fonction , qui est négative sur ces deux intervalles.
Elle est donc décroissante sur l'intervalle et sur l'intervalle .
Représentation graphique
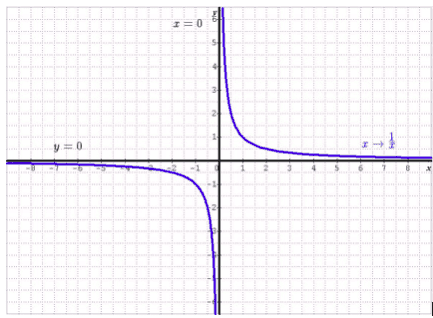
Sa représentation graphique (en bleu) est une hyperbole.
C’est une fonction impaire : sa représentation graphique est symétrique par rapport à l’origine du repère.
Asymptotes à la courbe
- Quand tend vers ou , on observe que tend vers 0.
On dit que la droite d’équation (axe des abscisses) est une asymptote horizontale à la courbe représentative de la fonction inverse. - Quand tend vers 0 (par valeurs inférieures ou supérieures), on observe que tend vers ou .
On dit que la droite d’équation (axe des ordonnées) est une asymptote verticale à la courbe représentative de la fonction inverse.