Bit et Octet
Les systèmes numériques stockent et manipulent l’information uniquement sous forme binaire. Le bit est la plus petite information pouvant être manipulée par un système numérique, elle ne peut prendre que deux valeurs : 0 ou 1. Un octet est un assemblage de 8 bits.
On peut utiliser les multiples habituels (G, M et k) pour les grandes quantités de données.
- 1 kbit = 1 000 bits ; 1 Mbit = 1 000 000 bits ; 1 Gbit = 1 000 000 000 bits
- 1 ko = 1 000 octets ; 1 Mo = 1 000 000 octets ; 1 Go = 1 000 000 000 octets
Conversion binaire – décimale
Les humains notent les nombres en décimal, avec 10 symboles. Les systèmes numériques utilisent les nombres sous forme binaire, avec 2 symboles. Il est donc fréquent de devoir convertir un nombre binaire en décimal, et inversement.
Méthode pour passer d’un nombre binaire à sa valeur décimale :
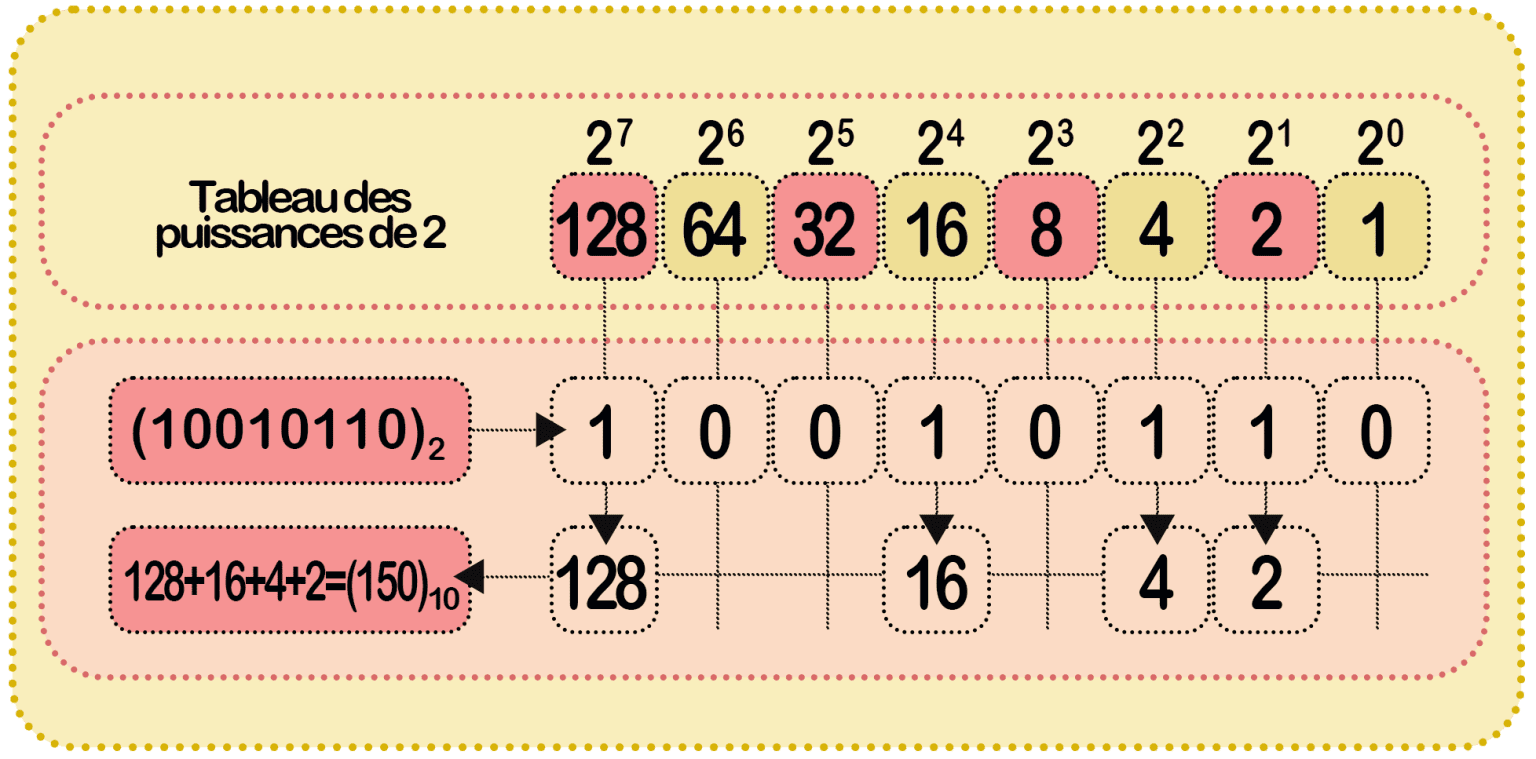
Méthode pour passer d’un nombre décimal à sa valeur binaire :
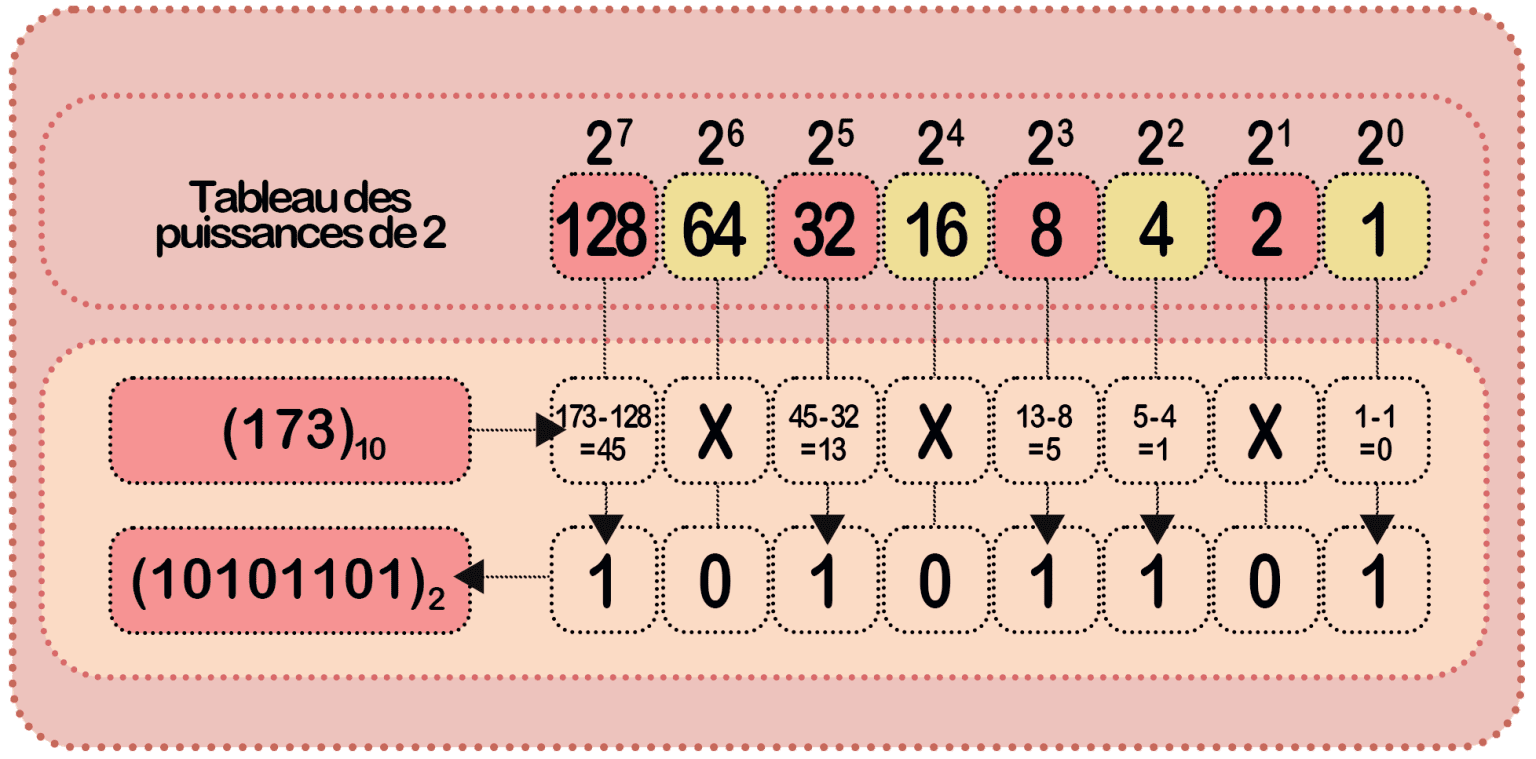
Conversion binaire – hexadécimale
Il existe une autre notation des nombres, très utilisée en informatique, l’hexadécimal. Cette notation utilise 16 symboles, dont voici la correspondance avec la notation binaire et la notation décimale :
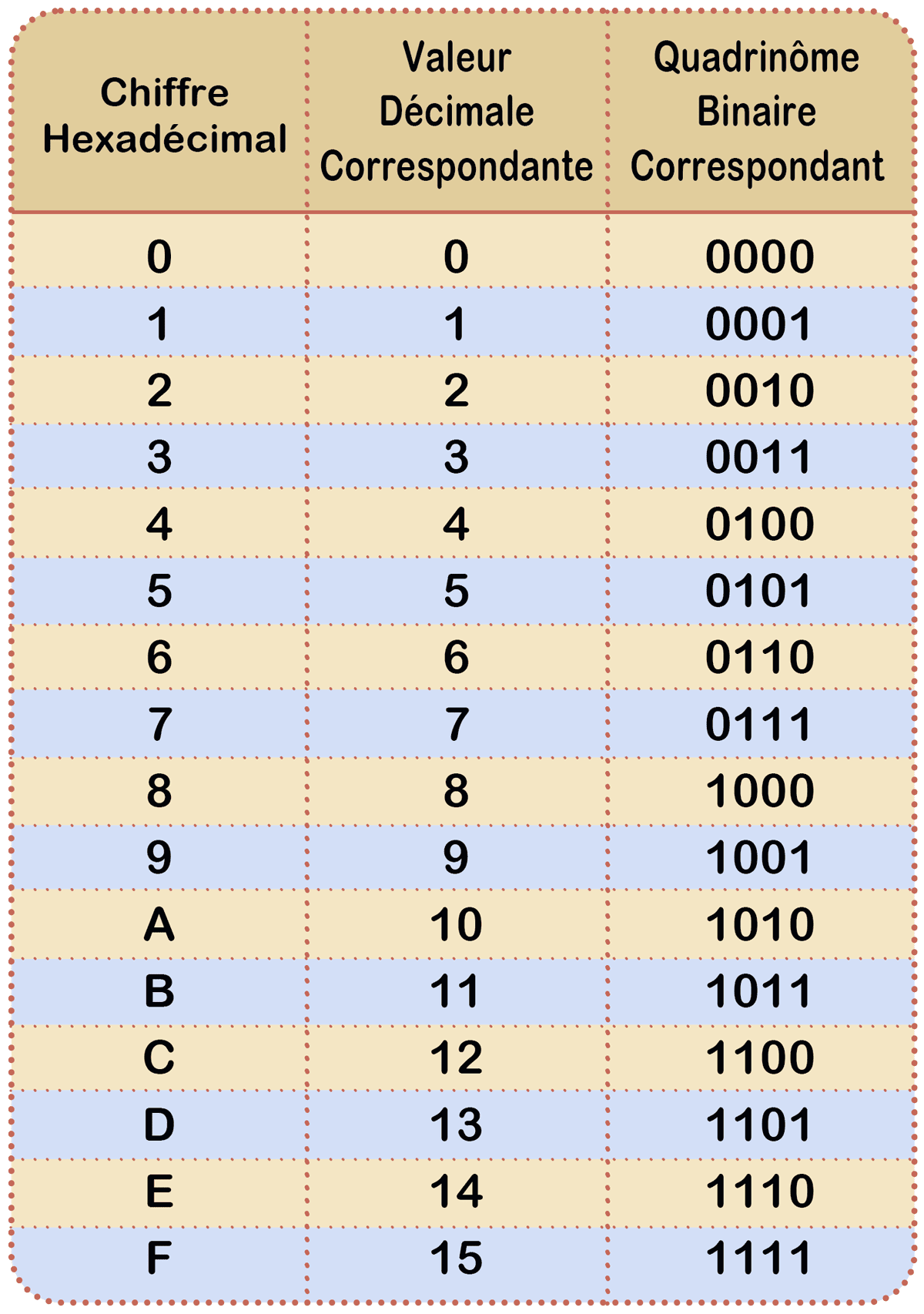
Il est aussi fréquent de devoir convertir un nombre binaire en hexadécimal, et inversement. Pour cela, on remarquera, grâce au tableau de correspondance, que 4 chiffres binaires correspondent exactement à 1 chiffre hexadécimal.
Méthode pour passer d’un nombre binaire à sa valeur hexadécimale :

Méthode pour passer d’un nombre hexadécimal à sa valeur binaire :
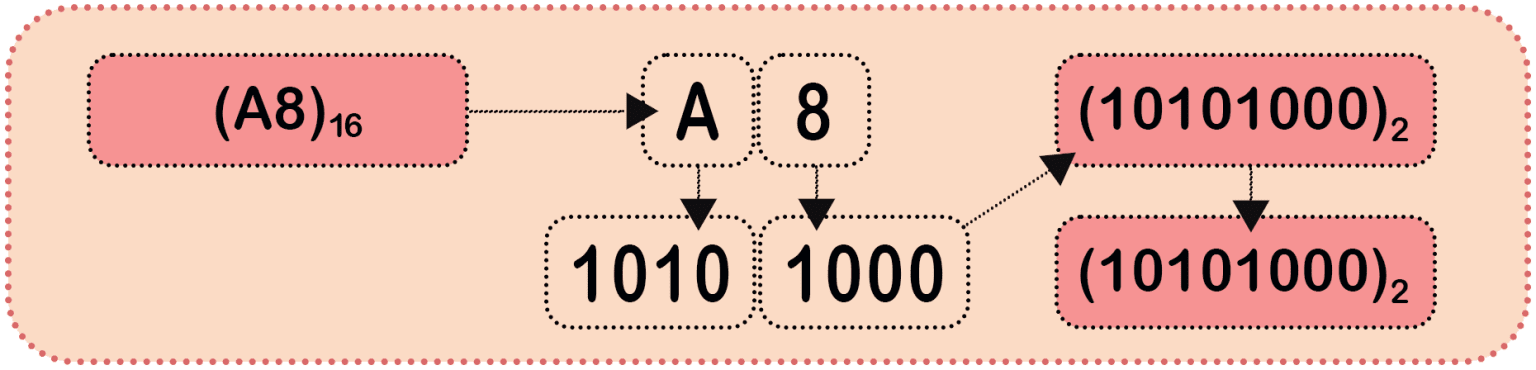
Encodage du Texte
Le texte est aussi stocké par les systèmes numériques sous forme binaire. Chaque caractère textuel correspond à un code binaire.
La traduction du texte au binaire se fait grâce à une table de conversion, comme la table ASCII ou le format UTF-8.
Exemple - extrait de la table ASCII :